In a previous post,we looked at the Platonics as portions were cut off (truncated). There are four objects that are made from further removal of edges/corners.
Unfortunately, these are not “perfect” truncations.
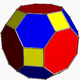
If you take a cuboctahedron and cut off each corner at the midpoint of each edge, you then end up with smaller triangle faces ¼th the original area and inverted and smaller squares ½ the original area and rotated 45°. You also get 12 new faces that are rectangles. This does not fit the definition of a “regular polyhedron” as rectangles are not regular polygons, they have sides that are of different lengths.
In order to get this object to be regular, you have to distort it slightly to make the rectangles into squares. Then you have a small rhombicuboctahedron. It is called this because the faces lie in the same plane as the rhombic dodecahedron, the dual of the cuboctahedron. (No one ever said that mathematicians were good at naming things.)
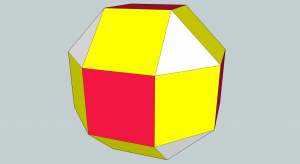
A better method of construction is a sort of “double truncation.” take a cube and chamfer all the edges at 45° where the cut is \((edge length\cdot [\sqrt2-1] )\) from each edge (Fig.1). You then truncate a second time cutting off each end of the elongated hexagons, meeting each square at the very tip of the corners, creating equilateral triangles (Fig.2).
Looking at any square face straight on, the object has the outline of a regular octagon, therefore the dihedral angle between any two squares is 135°.
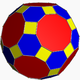
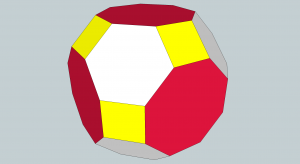
Likewise, you can cut off the corners of a cuboctahedron to turn the triangle faces into hexagons and square faces into octagons, but again the new faces are rectangles, not squares. Distortion will then give you a great rhombicuboctahedron. It is also called by some a truncated cuboctahedron.
The octagon-square dihedral angle is 135°.
The white faces of both are parallel to those of an octahedron, so both can also be made from chamfering an octahedron’s edges and truncating the corners.
Another two objects can be made starting with an icosidodecahedron, instead of a cuboctahedron, the small and great rhombicosidodecahedrons and truncating appropriately.
Regardless of how you construct the objects, all faces should be regular polygons and all edges are the same length.