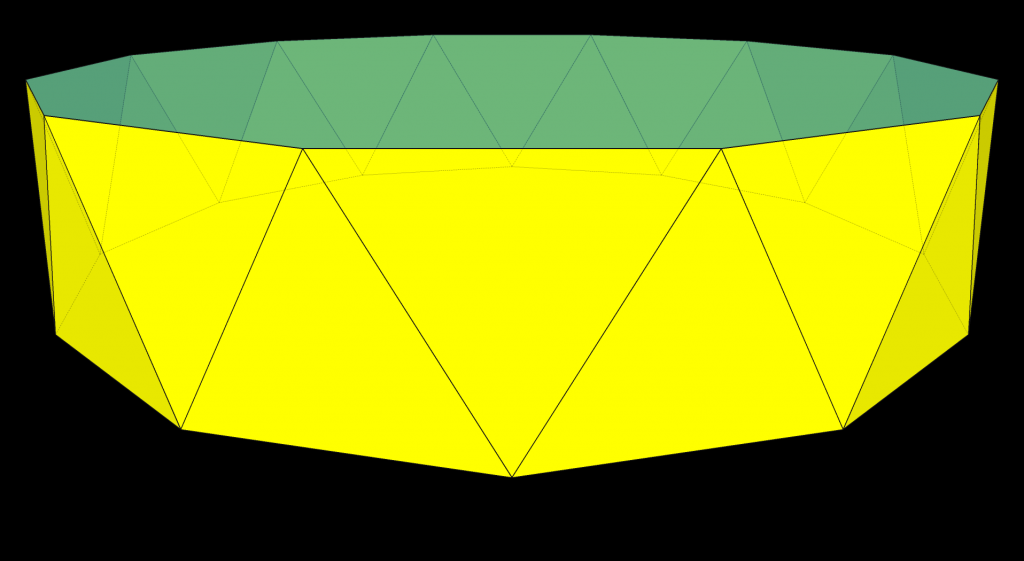
In geometry, a prism is a polyhedron with an n-sided polygonal base, another congruent parallel base (with the same rotational orientation), and n other faces (necessarily all parallelograms) joining corresponding sides of the two bases. Prisms are named for their base, so a prism with a pentagonal base is called a pentagonal prism.
In regular prisms, all side faces (all squares) are at right angles to the bases. The number of prisms is infinite, approaching a circular base.
The interior angles of the base faces is \(\frac{180(n-2)}{n}\), where n is the number of sides. This is really the only “difficult” math property of prisms.
Some prisms are not normally considered or called prisms, such as a square prism is just a cube.
|
|
|
|
|
If instead of connecting the bases with squares, you connect them with equilateral triangles, you then get antiprisms.
|
|
|
|
|
|
For n=2, the digonal antiprism is a degenerate case, as there is no base polygon, only a line segment. Otherwise the top face is a duplicate of the bottom, only rotated 180°/n.
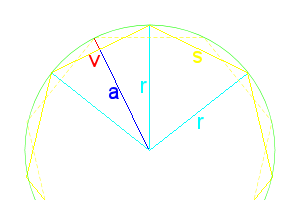 Figure 1: Polygon Dimensions |
For dihedral angles for antiprisms, things are a lot more complicated than prisms.
Lets start with looking at the base polygon, Figure 1.
A regular polygon always has the following properties:
$$\begin{align} radius\ r&=DB=\frac{s}{2\sin\frac{180^\circ}{n}} = \frac{a}{\cos\frac{180^\circ}{n}}
\\ apothem\ a &=\overline{DE}=r\cdot\cos\frac{180^\circ}{n}=\frac{s}{2\tan\frac{180^\circ}{n}}
\\ side\ s&=r\cdot2\sin\frac{180^\circ}{n}=a\cdot 2\tan\frac{180^\circ}{n}=AB=BC=FG
\\ angle\ \theta &=\frac{360^\circ}{n}
\\sagitta\ v&=r-a=r(1-\cos\frac{360}{2n})=r(2\sin^2\frac{360}{4n})=\frac{s(1-\cos\frac{360}{2n})}{2\sin\frac{360}{2n}}=\frac{s(\sin^2\frac{360}{4n})}{\sin\frac{360}{2n}}=s\frac12\tan\frac{90}{n}=\overline{BE}
\end{align}$$
The apothem is the distance from the center to the midpoint of any side. The difference between the radius and apothem is called the sagitta, also sometimes called the versine function (\(versin\ \mu=1-\cos\mu=2\sin^2\frac12\mu)\). The antiprism’s sides will be deflected away from 90° by the length of BE (or v). The dotted line is the location of the second base, always rotated θ/2 to that of the first base.
Normally it would be odd trying to calculate the radius of a circle, but we are defining our polygon based on its side length being one unit.
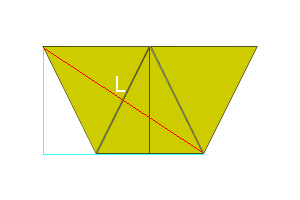 Figure 2 |
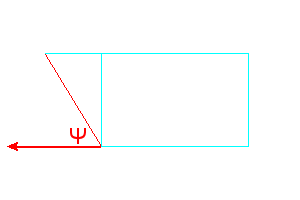 Figure 3 |
If we draw a line at the midpoint of each triangle all the way around, we get a regular polygon with 2n sides, parallel to each base.
The height of the triangle is line BE2, \(\frac{\sqrt3}{2}\). We do not yet know the height of the antiprism (\(\overline{E_1E_2}\)), but can find it.
$$\begin{align} (\overline{BE_1})^2+(\overline{E_1 E_2})^2 &=(\overline{BE_2})^2
\\ (\overline{E_1 E_2})^2 &=(\overline{BE_2})^2-(\overline{BE_1})^2
\\ &=\left(\frac{\sqrt3}{2}\right)^2-\left(s\frac12\tan\frac{90}{n}\right)^2
\\ &=\frac34-s^2\cdot\frac14\tan^2\frac{90}{n}
\\ &=\frac{3-s^2\tan^2\frac{90}{n}}{4}
\\ \overline{E_1 E_2} &=\frac12\sqrt{3-s^2\tan^2\frac{90}{n} }
\end{align}$$
This is as simplified as we can get without deciding on how many sides the base will have. The height of an antiprism must always be less than \(\frac12 s\sqrt3\), the height of a regular triangle.
Here are a few of the first heights for n:
| n | θ | Height |
| 2 | 45 | \(\frac1{\sqrt2}\) |
| 3 | 60 | \(\sqrt{\frac23}\) |
| 4 | 90 | \(\sqrt[4]{\frac12}\) |
| 5 | 36 | \(\sqrt{\frac{5+\sqrt5}{10}}\) |
| 6 | 30 | \(\sqrt{\sqrt3-1}\) |
| 8 | 22.5 | \(\sqrt{\sqrt{5+\frac{7\sqrt2}{2}} -1-\sqrt2}\) |
| 10 | 18 | \(\frac12\sqrt{-8-4\sqrt5-2(1+\sqrt5)\sqrt{5+2\sqrt5}}\) |
For the dihedral angles, ∠E1BE2 is the same as ∠Ψ, and \(\cos\angle BE_2D_2 =-\cos\angle\Psi\).
$$\begin{align} \cos\angle E_1BE_2 &=\frac{(BE_1)^2+(BE_2)^2-(E_1 E_2)^2}{2[(BE_1)(BE_2)]}
\\ &=\frac{\left(\frac12\tan\frac{90}{n}\right)^2+\left(\frac{\sqrt3}{2}\right)^2-\left(\frac12\sqrt{3-\tan^2\frac{90}{n} }\right)^2}{2\cdot\frac12\tan\frac{90}{n}\cdot\frac{\sqrt3}{2}}
\\ &=\frac{ \frac{\tan^2\frac{90}{n}}{4}+\frac34-\frac{3-\tan^2\frac{90}{n} }{4} }{\frac{\sqrt3}{2}\cdot\tan\frac{90}{n}}
\\ &=\frac{ \frac{2\tan^2\frac{90}{n}}{4} }{\frac{\sqrt3}{2}\cdot\tan\frac{90}{n}}=\frac{ \frac12\tan^2\frac{90}{n} }{\frac{\sqrt3}{2}\cdot\tan\frac{90}{n}}
\\ &= \frac{\tan^2\frac{90}{n}}{2} \cdot \frac{2}{\sqrt3\cdot\tan\frac{90}{n}}
\\ &= \frac{\tan^2\frac{90}{n}}{\sqrt3\cdot\tan\frac{90}{n}}
\\ &= \frac{\tan\frac{90}{n}}{\sqrt3}
\\ &= \frac1{\sqrt3}\cdot\tan\frac{90}{n}
\\ \cos\angle BE_2D_2&=-\frac1{\sqrt3}\cdot\tan\frac{90}{n}
\end{align}$$
Here are the first few dihedrals for n:
| n | \(\angle E_1BE_2\) | \(\angle BE_2D_2\) |
| 2 | 54.735° | 125.264° |
| 3 | 70.528° | 109.471° |
| 4 | 76.163° | 103.836° |
| 5 | 79.187° | 100.812° |
| 6 | 81.101° | 98.8994° |
| 8 | 83.405° | 96.5945° |
For the side-to-side dihedrals, let’s draw a line from point C, straight down, equal to the height, and call this point K. K is in the same plane as the bottom base. Looking at Figure 1, we can see that ∠KDF is \(\frac32\theta\), or \(\frac{540}{n}\). Connecting F and K, we get a line of \(2r\sin\frac{540}{2n}= s\cdot\frac{sin\frac{270}{n}}{\sin\frac{180}{n}}\). Note \(\overline{FK}\) is coplanar with G and E2, but does not go through either point.
We can now find the distance between C and F,
$$\begin{align} (CF)^2&=(CK)^2+(FK)^2
\\ &=\frac{3-s^2\tan^2\frac{90}{n}}{4} + s^2\cdot\frac{\sin^2\frac{270}{n}}{\sin^2\frac{180}{n}}
\\ (CF) &=\sqrt{\frac{3-s^2\tan^2\frac{90}{n}}{4} + s^2\cdot\frac{\sin^2\frac{270}{n}}{\sin^2\frac{180}{n}} }
\end{align}$$
In Figure 2, we see that \(CL=LF=BE_2=\frac{\sqrt3}{2}\). We can now find ∠CLF, the dihedral, with s=1 factored out,
$$\begin{align} \cos\angle CLF &=\frac{(CL)^2+(LF)^2- (CF)^2}{2\cdot CL\cdot LF}
\\ &=\frac{(\frac{\sqrt3}{2})^2+(\frac{\sqrt3}{2})^2-(CF)^2 }{2\cdot (\frac{\sqrt3}{2})(\frac{\sqrt3}{2})}
\\ &=\frac{\frac34+\frac34-(CF)^2 }{\frac32}
\\ &=\left[\frac64-(CF)^2\right]\div\frac32=\left[\frac32-(CF)^2\right]\cdot\frac23
\\ &=1-\frac23(CF)^2
\\ &=1-\frac23\left(\frac{3-\tan^2\frac{90}{n}}{4} + \frac{\sin^2\frac{270}{n}}{\sin^2\frac{180}{n}} \right)
\end{align}$$
Multiplying out the CF2 is really messy, best to reduce the other parts as much as possible, then square.
Here are the first few dihedral angles for n:
| n | \(\cos\angle CLF\) | ∠CLF |
| 2 | \(\frac13\) | 70.528779 |
| 3 | \(-\frac13\) | 109.47122 |
| 4 | \(\frac{1-2\sqrt2}{3}\) | 127.552 |
| 5 | \(-\frac{\sqrt5}{3}\) | 138.189685 |