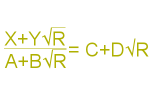Quite often, when doing calculations on polyhedra, you will find yourself with complex equations like $$\begin{equation}\tag{eq1}\label{eq1}\frac{20+7\sqrt3}{1+2\sqrt3}\end{equation}$$

Is the top evenly divisible by the bottom? I certainly can’t tell just by looking at them.

There must be a method to factor the numerator.

Let’s start with $$\color{blue}{(A+B\sqrt{R})}\color{lime}{(C+D\sqrt{R})}$$ multiplying the terms together gives $$\color{salmon}{AC+BRD+(BC+AD)\sqrt{R}}$$

So, $$\frac{\color{salmon}{AC+BRD+(BC+AD)\sqrt{R}}}{\color{blue}{A+B\sqrt{R}}} = \color{lime}{C+D\sqrt{R}}$$

Then we can substitute known values (A=1, B=2, R=3) into the formula. $$\frac{1C+2(3)D+(2C+1D)\sqrt{3}}{1+2\sqrt{3}} = C+D\sqrt{3}$$

Finding the answer is just a matter of finding C and D.

Consider that
$$\frac{\color{yellow}{C+6D} + \color{cyan}{(2C+D)}\sqrt3}{1+2\sqrt3} = \frac{\color{yellow}{20}+\color{cyan}{7}\sqrt3}{1+2\sqrt3}$$

We can break the equation into the colored sections to find $$\begin{align}\color{yellow}{C+6D} & \color{yellow}{=20} \\ C&=20-6D\tag{eq2}\label{eq2} \end{align}$$ and $$\color{cyan}{2C+D = 7}\tag{eq3}\label{eq3}$$

We now know C \eqref{eq2}, at least in terms of D, then substitute this into \eqref{eq3}.
$$\begin{align}2(20-6D)+D &= 7 \\ 40-12D+D &= 7 \\ -11D &= 7-40 = -33 \\D &= \frac{-33}{-11} \\ D&=3\end{align}$$

Returning to \eqref{eq2} and substituting D=3, we get \(C = 20-6\cdot 3 = 20-18 = 2\).

Then our answer should be \(2+3\sqrt{3}\), and it is, because \((1+2\sqrt3)(2+3\sqrt3) = 20+7\sqrt3\).

This method make it simple to divide out these complicated numbers, although, you might not get a simpler answer. For example, if we change \eqref{eq1} to \(\Large\frac{19+7\sqrt3}{1+2\sqrt3}\), we end up with answers C=23/11 and D=31/11, but it still works as \((1+2\sqrt3)(\frac{23}{11}+\frac{31\sqrt3}{11}) = 19+7\sqrt3\). Although, we could write our answer as \(\frac{1}{11}(23+31\sqrt3)\).

Another example:$$\frac{-3}{3+2\sqrt3}$$
We have values (A=3, B=2, R=3), giving $$3C + 2\cdot3D + (2C+3D)\sqrt3 = (3+2\sqrt3)(C+D\sqrt3)$$

Remember that \(-3\) is the same as \(-3+0\sqrt3\). So
$$\begin{align}3C+6D&=-3\label{e2}\tag{eq4}\\
2C+3D&=0\label{e3}\tag{eq5}
\end{align}$$

Working out \eqref{e2} gives
$$\begin{align}3C+6D&=-3 \\ 6D&= -3-3C \\D&=\frac{3(-1-C)}{6} \\D&= \frac{-1-C}{2}\end{align}$$

Plugging into \eqref{e3}, gives
$$\begin{align}2C+3D&=0 \\ 2C+3\cdot(\frac{-1-C}{2})&=0 \\ \frac{4C}{2}+\frac{-3C-3}{2}&=0 \\ \frac{4C-3C-3}{2}&=0 \\ \frac{C-3}{2}&=0 \\ C-3&=0 \\C&=3\end{align}$$

With C=3, we can find D in \eqref{e2} $$\begin{align}3(3)+6D&=-3 \\ 9+6D&=-3 \\ 6D&=-3-9 \\ 6D&=-12 \\ D&=\frac{-12}{6} \\ D&=-2\end{align}$$

So the answer is \(3-2\sqrt3\), as \((3+2\sqrt3)(3-2\sqrt3)=-3\).

You might notice this is the same as the “Difference of 2 squares” (x-y)(x+y) = x²-xy+xy-y² = x²-y². The “xy” terms cancel each other out, leaving 0. (x-y) and (x+y) are conjugates of one another, so when you have a numerator with a zero times the square root (or in other words, the numerator is a whole number), you may wish to try the denominator’s conjugate first. It may not be the answer you seek, but it can help you sometimes.

If the denominator is a whole number (or rational), $$\frac{6+2\sqrt3}{-2}$$

then divide both parts of the numerator by the denominator,

$$\frac{6}{-2}+\frac{2\sqrt3}{-2}=-3-\sqrt3$$

So to find an answer to $$\notag\frac{X+Y\sqrt{R}}{A+B\sqrt{R}} = C+D\sqrt{R}$$

You will need to find the solutions to \(AC+BRD=X\) and \(BC+AD=Y\)

UPDATE: I have also realized that you can just multiply the top and bottom of the fraction by the denominator’s conjugate.

In the first equation:

$$\begin{align}\frac{20+7\sqrt3}{1+2\sqrt3}&=\frac{(20+7\sqrt3)(1-2\sqrt3)}{(1+2\sqrt3)(1-2\sqrt3)}\\&=\frac{20-42+7\sqrt3-40\sqrt3}{1-12}\\&=\frac{-22-33\sqrt3}{-11}\\&=2+3\sqrt3\end{align}$$

In this method, the denominator is always a whole number (if both A&B are whole numbers).