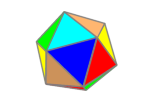
 The icosahedron has 12 equilateral triangles as faces.
The icosahedron has 12 equilateral triangles as faces.
It can be split into 3 parts, a pentagonal anti-prism and two pentagonal pyramids. We will start by looking at a pentagonal pyramid.
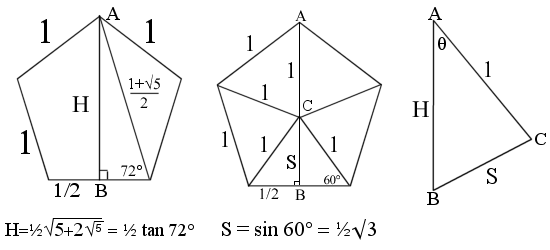
We have already done most of the work earlier.
To find ∠ACB,
$$\begin{align}\cos \angle ACB &= \frac{1^2 + S^2 – H^2}{2\cdot1\cdot S}\\
&= \frac{1^2 + \frac34 – \frac{5+2\sqrt5}{4}}{2\cdot 1\cdot \frac{\sqrt3}{2}}\\
&= \frac{\frac{2-2\sqrt5}{4} }{\sqrt3} \\
&= \frac{2-2\sqrt5}{4\sqrt3} \\
&= \frac{1-\sqrt5}{2\sqrt3}\\ACB &= 110.905157\ldots^\circ \end{align}$$
This is the vertex angle from one face to the opposite edge.
Taking two triangle faces that are abutting, the tips would be Phi (Φ) apart, you can draw a triangle of sides S, S, and Φ, going through the center of each equilateral triangle and the tips.
$$\begin{align}Icosahedron\ Dihedral \angle &= \cos^{-1}\Bigg(\frac{S^2 + S^2 – \Phi^2}{2\cdot S\cdot S}\Bigg)\\
&=\cos^{-1}\Bigg(\frac{ \frac34 + \frac34 – \frac{6+2\sqrt5}{4} }{ 2\cdot \frac{\sqrt3}{2} \cdot \frac{\sqrt3}{2} }\Bigg)\\
&=\cos^{-1}\Bigg(\frac{ – \frac{2\sqrt5}{4} }{ 2\cdot \frac34 }\Bigg)\\
&=\cos^{-1}\Bigg(\frac{ – 2\sqrt5 }{ 2\cdot 3 }\Bigg)\\
&=\cos^{-1}\Bigg(\frac{-\sqrt5}{3}\Bigg)\\
&= 138.1896851\ldots^\circ \end{align}$$