The Archimedean solids are symmetric semi-regular polyhedra made of two or three regular polygons that meet at identical vertices. There are 13 Archimedean solids plus two mirror image forms.
Five of these are made by taking a Platonic Solid and truncating (cutting off) a regular triangular, square, or pentagonal pyramid from each corner.
Here the vertex configuration refers to the type of regular polygons that meet at any given vertex. For example, a vertex configuration of (4.6.8) means that a square, hexagon, and octagon meet at a vertex (with the order taken to be clockwise around the vertex).
Images are from Wikipedia.org.
| Name (Vertex configuration) |
Shape | Faces | Edges | Vertices | ||||
|---|---|---|---|---|---|---|---|---|
| truncated tetrahedron (3.6.6) |
 |
8 | 4 triangles 4 hexagons |
18 | 12 | |||
| cuboctahedron (3.4.3.4) |
 |
14 | 8 triangles 6 squares |
24 | 12 | |||
| truncated cube (3.8.8) |
 |
14 | 8 triangles 6 octagons |
36 | 24 | |||
| truncated octahedron (4.6.6) |
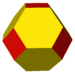 |
14 | 6 squares 8 hexagons |
36 | 24 | |||
| small rhombicuboctahedron (3.4.4.4 ) |
 |
26 | 8 triangles 18 squares |
48 | 24 | |||
| great rhombicuboctahedron (4.6.8) |
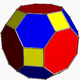 |
26 | 12 squares 8 hexagons 6 octagons |
72 | 48 | |||
| snub cube (2 chiral forms) (3.3.3.3.4) |
 |
38 | 32 triangles 6 squares |
60 | 24 | |||
| icosidodecahedron (3.5.3.5) |
 |
32 | 20 triangles 12 pentagons |
60 | 30 | |||
| truncated dodecahedron (3.10.10) |
 |
32 | 20 triangles 12 decagons |
90 | 60 | |||
| Truncated icosahedron (5.6.6 ) |
 |
32 | 12 pentagons 20 hexagons |
90 | 60 | |||
| small rhombicosidodecahedron (3.4.5.4) |
 |
62 | 20 triangles 30 squares 12 pentagons |
120 | 60 | |||
| great rhombicosidodecahedron (4.6.10) |
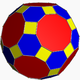 |
62 | 30 squares 20 hexagons 12 decagons |
180 | 120 | |||
| snub dodecahedron or snub icosidodecahedron (2 chiral forms) (3.3.3.3.5) |
 |
92 | 80 triangles 12 pentagons |
150 | 60 | |||