Phi $(\mathrm{\Phi },\varphi )$ is a Greek letter that mathematicians have assigned to a specific ratio or proportion, called the golden ratio, that most people find to be attractive in art, architecture, and nature.

The golden ratio is illustrated as $\frac{A}{B}=\frac{A+B}{A}\equiv \varphi$.

The only positive solution is ${\displaystyle \varphi =\frac{1+\sqrt{5}}{2}}$=1.6180339887498948482045868…

Many items have this ratio embedded into their design, by choice or coincidence, such as; the Parthenon, credit cards, corporate logos, the Mona Lisa, and the layout of Quincy Park in Cambridge, MA.

I find that there is some differences in the usage of symbols to represent the golden ratio. The most common is to use phi, either Φ(capitol), $\varphi$ (lower case), or φ (lower case variant), while Ø (Scandinavian O-slash) is often seen where non-Latin fonts are unusable or unavailable. Normally, one symbol will be used for the golden ratio and another for the inverse. Others will use “Phi” and “phi”, I don’t like this method as it is too difficult in many fonts to easily distinguish. The negative inverse is called the golden ratio conjugate and is sometimes represented with the upper/lower case letter that is not used for the golden ratio.

On this page, I will use the word “phi” or the symbol $\varphi ,$ as this is the symbol that Latex gives for phi. For the inverse, I will use ${\displaystyle \frac{1}{\varphi }}$ or ${\varphi }^{-1}$, as additional symbols are not really needed.

Some interesting relationships of phi:
$$\begin{array}{rl}\varphi +1={\varphi }^2& =2.6180339887498948482045868\dots \\ \varphi -1& =\frac{1}{\varphi }\\ \varphi & =1+\frac{1}{\varphi }\\ \frac{1}{\varphi }=\frac{-1+\sqrt{5}}{2}& =0.6180339887498948482045868\dots \\ {\left(\frac{1}{\varphi }\right)}^2& =1-\frac{1}{\varphi }\\ {\varphi }^3& =1+2\varphi \end{array}$$

Compare the decimal portion of $\varphi$ to that of ${\displaystyle \frac{1}{\varphi }}$. They are the same, as is ${\varphi }^2$.

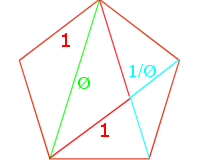
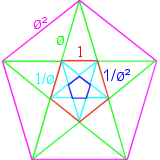
Pentagons and pentagrams show many signs of a relationship with phi. Notice in the pentagon, there is a red parallelogram (rhombus) with long diagonal of phi and side length 1. The height of the pentagon is the height of each of the arms of the star, a ($\varphi$,$\varphi$,1) isosceles triangle. Each line is the same length as the other lines of the same color, relatively speaking.

The pentagram is ${\varphi }^2$ times larger than a pentagram inscribed inside the pentagon. This relationship continues, every nested pentagon and pentagram is ${\varphi }^2$ times larger than the previous same shape and is ${\displaystyle \frac{1}{{\varphi }^2}}$times the next same shape.

The “kite” and “dart” of Penrose tiles can be merged to form the same rhombus. Penrose tiles are also found in the formation of the newly discovered quasi-crystals.

If  ${\varphi }^2=\varphi +1$, then $$\begin{array}{rl}{\varphi }^3& =\varphi \cdot {\varphi }^2\\ & =\varphi (\varphi +1)\\ & ={\varphi }^2+\varphi \\ & =\varphi +1+\varphi \\ & =1+2\varphi \end{array}$$

Therefore $$\begin{array}{rl}{\varphi }^4& =\varphi \cdot {\varphi }^3\\ & =\varphi (1+2\varphi )\\ & =\varphi +2{\varphi }^2\\ & =\varphi +2(1+\varphi )\\ & =\varphi +2+2\varphi \\ & =2+3\varphi \end{array}$$

This shows an important and remarkable pair of results for all integers N:

$${\varphi }^N={\varphi }^{N-1}+{\varphi }^{N-2}$$

$${\left(\frac{1}{\varphi }\right)}^N={\left(\frac{1}{\varphi }\right)}^{N+1}+{\left(\frac{1}{\varphi }\right)}^{N+2}$$

A quick table of values:

${\varphi }^N$	$\frac{1}{2}\cdot (a+b\sqrt{5})$	$c+d\varphi$	$j+k\frac{1}{\varphi }$	approximate value
10	$\frac{1}{2}(115+55\sqrt{5})$	$34+55\varphi$	$89+55\frac{1}{\varphi }$	122.9918
9	$\frac{1}{2}(68+34\sqrt{5})$	$21+34\varphi$	$55+34\frac{1}{\varphi }$	76.01315
8	$\frac{1}{2}(47+21\sqrt{5})$	$13+21\varphi$	$34+21\frac{1}{\varphi }$	46.97871
7	$\frac{1}{2}(29+13\sqrt{5})$	$8+13\varphi$	$21+13\frac{1}{\varphi }$	29.03444
6	$\frac{1}{2}(18+8\sqrt{5})$	$5+8\varphi$	$13+8\frac{1}{\varphi }$	17.94427
5	$\frac{1}{2}(11+5\sqrt{5})$	$3+5\varphi$	$8+5\frac{1}{\varphi }$	11.09016
4	$\frac{1}{2}(7+3\sqrt{5})$	$2+3\varphi$	$5+3\frac{1}{\varphi }$	6.85410
3	$\frac{1}{2}(4+2\sqrt{5})$	$1+2\varphi$	$3+2\frac{1}{\varphi }$	4.23606
2	$\frac{1}{2}(3+1\sqrt{5})$	$1+1\varphi$	$2+1\frac{1}{\varphi }$	2.61803
1	$\frac{1}{2}(1+1\sqrt{5})$	$0+1\varphi$	$1+1\frac{1}{\varphi }$	1.61803
0	$\frac{1}{2}(2+0\sqrt{5})$	$1+0\varphi$	$1+0\frac{1}{\varphi }$	1.00000
-1	$\frac{1}{2}(-1+1\sqrt{5})$	$-1+1\varphi$	$0+1\frac{1}{\varphi }$	0.61803
-2	$\frac{1}{2}(3-1\sqrt{5})$	$2-1\varphi$	$1-1\frac{1}{\varphi }$	0.09016
-3	$\frac{1}{2}(-4+2\sqrt{5})$	$-3+2\varphi$	$-1+2\frac{1}{\varphi }$	0.05572
-4	$\frac{1}{2}(7-3\sqrt{5})$	$5-3\varphi$	$2-3\frac{1}{\varphi }$	0.03444
-5	$\frac{1}{2}(-11+5\sqrt{5})$	$-8+5\varphi$	$-3+5\frac{1}{\varphi }$	0.02128
-6	$\frac{1}{2}(18-8\sqrt{5})$	$13-8\varphi$	$5-8\frac{1}{\varphi }$	0.05572

Note: values in the last column are truncated, not exact, and column 2 fractions are not simplified, to show pattern.

If we look at the integers in the third and fourth columns, you may notice a pattern emerge. They are all Fibonacci numbers (0, 1, 1, 2, 3, 5, 8, 13, …), where each number is the sum of the previous 2 numbers in the sequence. This gives us ${\varphi }^N={\left(\frac{1}{\varphi }\right)}^{-N}=F_{(N-1)}+F_N\cdot \varphi =F_{(N+1)}+F_N\cdot \frac{1}{\varphi }$, where $F_N$ is the $N^{th}$ Fibonacci number.

We also get the value ${\varphi }^N=\frac{1}{2}[F_{(N+1)}+F_{(N-1)}+F_N\cdot \sqrt{5}]$.

The integers multiplied by √5 in the second column, are also the Fibonacci numbers, but the first set are what is known as the Lucas number series. The Lucas numbers are just like the Fibonacci numbers, each is the sum of the previous 2 numbers, but instead of starting with 0 and 1, François Édouard Anatole Lucas started his series with 2 and 1.

The sequence of Lucas numbers begins: 2, 1, 3, 4, 7, 11, 18, 29, 47, 76, 123, …

Each series can be back calculated to find previous numbers, ultimately leading to alternating positive and negative numbers, as seen in the formulas for the negative powers of phi in the table.

Lucas numbers are of some use in primality testing.

If you take sequential Fibonacci numbers and divide one by the previous, i.e. $\frac{F_{(N+1)}}{F_{(N)}}$, the result becomes closer and closer to equaling $\varphi$ the higher N becomes, or $\frac{-1}{\varphi }$ the lower N becomes.

Interestingly, 8 and 144 are the only non-trivial perfect powers, being 2^3 and 12^2, respective.

Starting with 5, every second Fibonacci number is the length of the hypotenuse of a right triangle with integer sides, or in other words, the largest number in a Pythagorean triple, (3,4,5), (5,12,13), (16,30,34), (39,80,89), etc.

Update: Here are a few ways you can enter phi. If you hold the Alt key, type 232 on the numeric keypad, then release the Alt key, you get Φ (capitol phi).  Alt 237 gives φ (lower phi). In HTML, you can use Φ or Φ for uppercase, φ or φ for lower. These methods both work in the comments box.

If you need the square root radical or an exponent:

• √ – Alt 251
• ⁿ – Alt 252
• ± – Alt 0177
• ² – Alt 0178
• ³ – Alt 0179
• ¹ – Alt 0185

You can also use the Character Map program (in menu Start→Programs→Accessories→System Tools) to select and copy into the clipboard, although fonts may be unavailable on a different computer. Arial should be safe to use.