Table of exact trigonometric functions

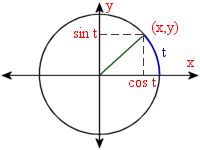
Since I noticed I had to keep looking some of these up, I place them here, just for reference, gathered from around the internet. Many of these formulas can be written in different ways, but I have simplified them as much as possible.

Where, $\varphi =\frac{1+\sqrt{5}}{2}=1.6180339887498948482045868\dots$, also known as the golden ratio (phi).

a		sin(a) = cos(b) = sin(90-b) = cos(90-a)	tan(a) = cot(b) = tan(90-b) = cot(90-a)	b
deg	rad			deg	rad
0	0	0	0	90	π/2
3	π/60	$\frac{1}{16}[(2-2\sqrt{3})\sqrt{5+\sqrt{5}}+\sqrt{2}(-1+\sqrt{5})(1+\sqrt{3})]$	$\frac{1}{4}[(2-\sqrt{3})(3+\sqrt{5})-2][2-\sqrt{10-2\sqrt{5}}]$	87	29π/30
6	π/30	$\frac{1}{8}[\sqrt{30-6\sqrt{5}}-\sqrt{5}-1]$	$\frac{1}{2}[\sqrt{10-2\sqrt{5}}-\sqrt{3}(-1+\sqrt{5})]$	84	7π/15
9	π/20	$\frac{1}{2}\sqrt{2-\sqrt{2+\varphi }}=\frac{1}{2}\sqrt{2-\sqrt{\frac{5+\sqrt{5}}{2}}}$	$1+\sqrt{5}-\sqrt{5+2\sqrt{5}}$	81	9π/20
12	π/15	$\frac{1}{8}[\sqrt{10+2\sqrt{5}}-\sqrt{3}(-1+\sqrt{5})]$	$\frac{1}{2}[\sqrt{3}(3-\sqrt{5})-\sqrt{2(25-11\sqrt{5})}]$	78	13π/30
15	π/12	$\frac{\sqrt{6}-\sqrt{2}}{4}=\frac{\sqrt{2-\sqrt{3}}}{2}$	$2-\sqrt{3}$	75	5π/12
18	π/10	$\frac{1}{2\varphi }=\frac{1}{1+\sqrt{5}}=\frac{\sqrt{5}-1}{4}$	$\frac{1}{5}\sqrt{25-10\sqrt{5}}$	72	2π/5
21	7π/60	$\frac{1}{16}[2(\sqrt{3}+1)\sqrt{5-\sqrt{5}}-\sqrt{2}(\sqrt{3}-1)(1+\sqrt{5})]$	$\frac{1}{4}[2-(2+\sqrt{3})(3-\sqrt{5})][2-\sqrt{2(5+\sqrt{5})}]$	69	23π/60
22.5	π/8	$\frac{1}{2}\sqrt{2–\sqrt{2}}$	$\sqrt{2}–1$	67.5	3π/8
24	2π/15	$\frac{1}{8}[-\sqrt{10-2\sqrt{5}}+\sqrt{3}(1+\sqrt{5})]$	$\frac{1}{2}[-\sqrt{3}(3+\sqrt{5})+\sqrt{2(25+11\sqrt{5})}]$	66	11π/30
27	3π/20	$\frac{1}{2}\sqrt{2-\sqrt{2-\frac{1}{\varphi }}}=\frac{1}{2}\sqrt{2-\sqrt{\frac{5-\sqrt{5}}{2}}}$	$-1+\sqrt{5}-\sqrt{5-2\sqrt{5}}$	63	7π/20
30	π/6	$\frac{1}{2}$	$\frac{1}{\sqrt{3}}$	60	π/3
33	11π/60	$\frac{1}{16}[2(\sqrt{3}-1)\sqrt{5+\sqrt{5}}+\sqrt{2}(1+\sqrt{3})(\sqrt{5}-1)]$	$\frac{1}{4}[2-(2-\sqrt{3})(3+\sqrt{5})][2+\sqrt{2(5-\sqrt{5})}]$	57	19π/60
36	π/5	$\frac{1}{2}\sqrt{3-\varphi }=\sqrt{\frac{5-\sqrt{5}}{8}}$	$\sqrt{5-2\sqrt{5}}$	54	3π/10
39	13π/60	$\frac{1}{16}[2(1-\sqrt{3})\sqrt{5-\sqrt{5}}+\sqrt{2}(\sqrt{3}+1)(\sqrt{5}+1)]$	$\frac{1}{4}[(2-\sqrt{3})(3-\sqrt{5})-2][2-\sqrt{2(5+\sqrt{5})}]$	51	17π/60
42	7π/30	$\frac{1}{8}[\sqrt{30+6\sqrt{5}}-\sqrt{5}+1]$	$\frac{1}{2}[-\sqrt{10+2\sqrt{5}}+\sqrt{3}(1+\sqrt{5})]$	48	4π/15
45	π/4	$\frac{1}{\sqrt{2}}$	1	45	π/4
48	4π/15	$\frac{1}{8}[\sqrt{10+2\sqrt{5}}+\sqrt{3}(-1+\sqrt{5})]$	$\frac{1}{2}[\sqrt{3}(3-\sqrt{5})+\sqrt{2(25-11\sqrt{5})}]$	42	7π/30
51	17π/60	$\frac{1}{16}[2(1+\sqrt{3})\sqrt{5-\sqrt{5}}+\sqrt{2}(\sqrt{3}-1)(\sqrt{5}+1)]$	$\frac{1}{4}[(2+\sqrt{3})(3-\sqrt{5})-2][2+\sqrt{10+2\sqrt{5}}]$	39	13π/60
54	3π/10	$\frac{\varphi }{2}=\frac{1+\sqrt{5}}{4}$	$\frac{1}{5}\sqrt{25+10\sqrt{5}}$	36	π/5
57	19π/60	$\frac{1}{16}[2(\sqrt{3}+1)\sqrt{5+\sqrt{5}}+\sqrt{2}(1-\sqrt{3})(\sqrt{5}-1)]$	$\frac{1}{4}[2-(2+\sqrt{3})(3+\sqrt{5})][2-\sqrt{2(5-\sqrt{5})}]$	33	11π/60
60	π/3	$\frac{\sqrt{3}}{2}$	$\sqrt{3}$	30	π/6
63	7π/20	$\frac{1}{2}\sqrt{2+\sqrt{2-\frac{1}{\varphi }}}=\frac{1}{2}\sqrt{2+\sqrt{\frac{5-\sqrt{5}}{2}}}$	$-1+\sqrt{5}+\sqrt{5-2\sqrt{5}}$	27	3π/20
66	11π/30	$\frac{1}{8}[\sqrt{30-6\sqrt{5}}+\sqrt{5}+1]$	$\frac{1}{2}[\sqrt{10-2\sqrt{5}}+\sqrt{3}(-1+\sqrt{5})]$	24	2π/15
67.5	3π/8	$\frac{1}{2}\sqrt{2+\sqrt{2}}$	$\sqrt{2}+1$	22.5	π/8
69	23π/60	$\frac{1}{16}[2(\sqrt{3}-1)\sqrt{5-\sqrt{5}}+\sqrt{2}(\sqrt{3}+1)(1+\sqrt{5})]$	$\frac{1}{4}[2-(2-\sqrt{3})(3-\sqrt{5})][2+\sqrt{2(5+\sqrt{5})}]$	21	7π/60
72	2π/5	$\frac{\sqrt{2+\varphi }}{2}=\frac{\sqrt{5+\sqrt{5}}}{2\sqrt{2}}$	$\sqrt{5+2\sqrt{5}}$	18	π/10
75	5π/12	$\frac{\sqrt{2+\sqrt{3}}}{2}$	$2+\sqrt{3}$	15	π/12
78	13π/30	$\frac{1}{8}[\sqrt{30+6\sqrt{5}}+\sqrt{5}-1]$	$\frac{1}{2}[\sqrt{10+2\sqrt{5}}+\sqrt{3}(1+\sqrt{5})]$	12	π/15
81	9π/20	$\frac{1}{2}\sqrt{2+\sqrt{2+\varphi }}=\frac{1}{2}\sqrt{2+\sqrt{\frac{5+\sqrt{5}}{2}}}$	$1+\sqrt{5}+\sqrt{5+2\sqrt{5}}$	9	π/20
84	7π/15	$\frac{1}{8}[\sqrt{10-2\sqrt{5}}+\sqrt{3}(1+\sqrt{5})]$	$\frac{1}{2}[\sqrt{3}(3+\sqrt{5})+\sqrt{2(25+11\sqrt{5})}]$	6	π/30
87	29π/30	$\frac{1}{16}[(2+2\sqrt{3})\sqrt{5+\sqrt{5}}+\sqrt{2}(-1+\sqrt{5})(-1+\sqrt{3})]$	$\frac{1}{4}[(2+\sqrt{3})(3+\sqrt{5})-2][2+\sqrt{10-2\sqrt{5}}]$	3	π/60
90	π/2	1	$\mathrm{\infty }$	0	0
deg	rad	sin(a) = cos(b) = sin(90-b) = cos(90-a)	tan(a) = cot(b) = tan(90-b) = cot(90-a)	deg	rad
a				b

$$\begin{array}{rllll}rad& deg& \sin & \cos & \tan \\ 2\pi & 360& 0& 1& 0\\ \pi & 180& 0& -1& 0\\ \frac{2\pi }{3}& 120& \frac{1}{2}\sqrt{3}& -\frac{1}{2}& -\sqrt{3}\\ \frac{\pi }{2}& 90& 1& 0& \pm \mathrm{\infty }\\ \frac{2\pi }{5}& 72& \frac{1}{4}\left(\sqrt{10+2\sqrt{5}}\right)& \frac{1}{4}(\sqrt{5}-1)& \sqrt{5+2\sqrt{5}}\\ \frac{\pi }{3}& 60& \frac{1}{2}\sqrt{3}& \frac{1}{2}& \sqrt{3}\\ \frac{\pi }{4}& 45& \frac{1}{2}\sqrt{2}& \frac{1}{2}\sqrt{2}& 1\\ \frac{2\pi }{9}& 40& \frac{i}{2}(\sqrt[3]{\frac{-1-\sqrt{-3}}{2}}-\sqrt[3]{\frac{-1+\sqrt{-3}}{2}})& \frac{1}{2}(\sqrt[3]{\frac{-1+\sqrt{-3}}{2}}+\sqrt[3]{\frac{-1-\sqrt{-3}}{2}})& \\ \frac{\pi }{5}& 36& \frac{1}{4}\left(\sqrt{10-2\sqrt{5}}\right)& \frac{1}{4}(\sqrt{5}+1)& \sqrt{5-2\sqrt{5}}\\ \frac{\pi }{6}& 30& \frac{1}{2}& \frac{1}{2}\sqrt{3}& \frac{1}{3}\sqrt{3}\\ \frac{\pi }{7}& & \frac{1}{24}\sqrt{3(112-\sqrt[3]{14336+\sqrt{-5549064193}}-\sqrt[3]{14336-\sqrt{-5549064193}})}& \frac{1}{24}\sqrt{3(80+\sqrt[3]{14336+\sqrt{-5549064193}}+\sqrt[3]{14336-\sqrt{-5549064193}})}& \\ \frac{2\pi }{15}& 24& \frac{1}{8}(\sqrt{15}+\sqrt{3}-\sqrt{10-2\sqrt{5}})& \frac{1}{8}(1+\sqrt{5}+\sqrt{30-6\sqrt{5}})& \frac{1}{2}(-3\sqrt{3}-\sqrt{15}+\sqrt{50+22\sqrt{5}})\\ \frac{\pi }{8}& 22.5& \frac{1}{2}\left(\sqrt{2-\sqrt{2}}\right)& \frac{1}{2}\left(\sqrt{2+\sqrt{2}}\right)& \sqrt{2}-1\\ \frac{\pi }{9}& 20& \frac{i}{4}(\sqrt[3]{4-4\sqrt{-3}}-\sqrt[3]{4+4\sqrt{-3}})& \frac{1}{4}(\sqrt[3]{4+4\sqrt{-3}}+\sqrt[3]{4-4\sqrt{-3}})& \\ \frac{\pi }{10}& 18& \frac{1}{4}(\sqrt{5}-1)& \frac{1}{4}\left(\sqrt{10+2\sqrt{5}}\right)& \frac{1}{5}\left(\sqrt{25-10\sqrt{5}}\right)\\ \frac{\pi }{12}& 15& \frac{1}{4}(\sqrt{6}-\sqrt{2})& \frac{1}{4}(\sqrt{6}+\sqrt{2})& 2-\sqrt{3}\\ \frac{\pi }{15}& 12& \frac{1}{8}[\sqrt{10+2\sqrt{5}}-\sqrt{3}(-1+\sqrt{5})]& \frac{1}{8}[\sqrt{30+6\sqrt{5}}+\sqrt{5}-1]& \\ \frac{\pi }{18}& 10& & & \\ \frac{\pi }{30}& 6& \frac{1}{8}[\sqrt{30-6\sqrt{5}}-\sqrt{5}-1]& \frac{1}{8}[\sqrt{10-2\sqrt{5}}+\sqrt{3}(1+\sqrt{5})]& \\ \frac{\pi }{40}& 4.5& \frac{1}{2}\sqrt{2-\sqrt{2+\sqrt{\frac{5+\sqrt{5}}{2}}}}& \frac{1}{2}\sqrt{2+\sqrt{2+\sqrt{\frac{5+\sqrt{5}}{2}}}}& \\ \frac{\pi }{45}& 4& & & \\ \frac{\pi }{60}& 3& \frac{1}{16}[(2-2\sqrt{3})\sqrt{5+\sqrt{5}}+\sqrt{2}(-1+\sqrt{5})(1+\sqrt{3})]& \frac{1}{16}[(2+2\sqrt{3})\sqrt{5+\sqrt{5}}+\sqrt{2}(-1+\sqrt{5})(-1+\sqrt{3})]& \\ \frac{\pi }{90}& 2& & & \\ \frac{\pi }{180}& 1& \frac{1}{2i}\left[\sqrt[3]{\cos (3^{\circ })+i\sin (3^{\circ })}–\sqrt[3]{cos(3^{\circ })–i\sin (3^{\circ })}\right]& & \end{array}$$

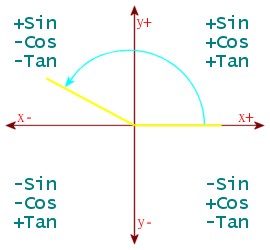
The values for angles outside the range 0-90 degrees, can be found by reducing the angle be in the correct range. Negative angles should have 360 added to them until positive. If angle ≥360, subtract multiples of 360 from it, until <360. Then, if angle ≥270, subtract from 360. If angle ≥180, subtract 180. If angle ≥90, subtract from 180.

Examples:

• sin(-54)=sin(360-54)=sin(306)=-sin(54)
• cos(120)=cos(180-120)=-cos(60)
• tan(225)=tan(225-180)=tan(45)
• tan(-225)=tan(360-225)=tan(135)=tan(180-135)=-tan(45)
• sin(1000)=sin(1000-360*2)=sin(280)=sin(360-280)=-sin(80)

Angles between 0 and 360 will have the following signs and are measured in a counter-clockwise arc originating at the “x+” line.

FYI, here is the exact value of sin 1°, $\frac{1}{2i}\left[\sqrt[3]{\cos (3)+i\sin (3)}–\sqrt[3]{cos(3)–i\sin (3)}\right]$, where $i=\sqrt{-1}$,

$$\begin{gathered} \frac{1}{2}(-1-i\sqrt{3})\sqrt[3]{-\frac{\sqrt{6}}{384}(\sqrt{5}-1)(3+\sqrt{3})+\frac{\sqrt{3}}{192}(3-\sqrt{3})\sqrt{5+\sqrt{5}}+\frac{i}{8}\sqrt{1-\frac{1}{48}{[\sqrt{6}(\sqrt{5}-1)(3+\sqrt{3})-2\sqrt{3}(3-\sqrt{3})\sqrt{5+\sqrt{5}}]}^2}}+ \\ \frac{1}{2}(-1+i\sqrt{3})\sqrt[3]{-\frac{\sqrt{6}}{384}(\sqrt{5}-1)(3+\sqrt{3})+\frac{\sqrt{3}}{192}(3-\sqrt{3})\sqrt{5+\sqrt{5}}-\frac{i}{8}\sqrt{1-\frac{1}{48}{(\sqrt{6}(\sqrt{5}-1)(3+\sqrt{3})-2\sqrt{3}(3-\sqrt{3})\sqrt{5+\sqrt{5}})}^2}} \end{gathered}$$

and the cos 1°,

$$\begin{gathered} \frac{1}{2}\sqrt{2-(i\sqrt{3}-1)\sqrt[3]{\frac{-\sqrt{3}}{64}(1+\sqrt{5})-\frac{\sqrt{2}}{128}(\sqrt{5}-1)\sqrt{5+\sqrt{5}}+\frac{i}{8}\sqrt{1-{[\frac{\sqrt{3}}{8}(1+\sqrt{5})+\frac{\sqrt{2}}{16}(\sqrt{5}-1)\sqrt{5+\sqrt{5}}]}^2}}+ \\ (i\sqrt{3}+1)\sqrt[3]{\frac{-\sqrt{3}}{64}(1+\sqrt{5})-\frac{\sqrt{2}}{128}(\sqrt{5}-1)\sqrt{5+\sqrt{5}}–\frac{i}{8}\sqrt{1-{[\frac{\sqrt{3}}{8}(1+\sqrt{5})+\frac{\sqrt{2}}{16}(\sqrt{5}-1)\sqrt{5+\sqrt{5}}]}^2}}} \end{gathered}$$