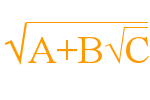
Lately, I have been doing a lot of math involving square roots of numbers added to square roots, in the form of \(\sqrt{A+B\sqrt{C}}\), this is called a “nested radical.” Normally, you would not be able to simplify any further, unless there was a common factor of both that could be removed, or if both items had the same number under the radical (eg. \(\sqrt{4\sqrt7+12\sqrt7}=\sqrt{16\sqrt7}=4\sqrt[4]{7}\) ).
I can take a number like \((1+\sqrt5)^2\) and work out it is equal to \(6 + 2\sqrt5\). Unfortunately, it is very difficult to recognize that \(1+\sqrt5\) is the square root (or even a factor) of that. Even harder, trying to find an equation such as \(\sqrt{469+144\sqrt5}\).
Recently, I found a method of breaking down the equation into its square root equation.
With an equation in the form of \(\sqrt{A+B\sqrt{C}}\), where C contains no perfect square factors, taking the formula \(D^2 = A^2 – (B^2)*C\), if D is a rational number, you will be able to factor the equation, otherwise it is simplified as much as is possible.
Then you will be able to get the formula: \(\sqrt{A+B\sqrt{C}} = \pm \left(\sqrt{\frac{A-D}{2}} + sign(A*B)*\sqrt{\frac{A+D}{2}}\right)\), where sign(A*B) is the positive or negative value of A*B, it will always give you 0, +1, or -1.
So to find \(\sqrt{469+144\sqrt5}\), we find \(469^2 – 144^2 * 5 = 116281\). Since 116281 = 341*341, we can plug D=341 into the formula to get:
$$\begin{align} \sqrt{\frac{469-341}{2}} + 1*\sqrt{\frac{469+341}{2}}&=\sqrt{\frac{128}{2}} + \sqrt{\frac{810}{2}}\\
&=\sqrt{64} + \sqrt{405} \\
&= 8 + \sqrt{81*5} \\
&= 8+9\sqrt{5}\end{align}$$
So, \(\sqrt{469+144\sqrt5} = (8+9\sqrt{5}) \text{ and } (-8-9\sqrt{5})\).
To find \(\sqrt{53-12\sqrt{11}}\), we find \(53^2 – 12^2 * 11 = 1225\). Since 1225 = 35*35, we can plug D=35 into the formula to get:
$$\begin{align*} \sqrt{\frac{53-35}{2}} + -1*\sqrt{\frac{53+35}{2}} &=\sqrt{\frac{18}{2}} – \sqrt{\frac{88}{2}}\\
&=\sqrt{9} – \sqrt{44} \\
&= 3 – \sqrt{4*11} \\
&= 3-2\sqrt{11} \end{align*}$$
So, \(\sqrt{53-12\sqrt11} = (3-2\sqrt{11}) \text{ and } (-3+2\sqrt{11})\).
If A and B have the same sign, the answer will have both terms the same sign ({+,+} and {-,-} are equally valid). If A and B have different signs, the terms in the answer will have different signs ({+,-} and {-,+}). Often you will need to determine the complete answer that equates to positive, after all, it is hard to have a real object with a negative length.
An interesting correlation: \((X-Y)^2 = (Y-X)^2\), but remember \(\sqrt{X-Y} \not= \sqrt{Y-X}\). Double check your signs by re-squaring your answer.
Note: This still works if D is not an integer, but is rational:
$$\begin{align*} \sqrt{8.41+2.64\sqrt5} &=\sqrt{\frac{8.41-5.99}{2}} + \sqrt{\frac{8.41+5.99}{2}} &D=\sqrt{8.41^2 + 2.64^2\cdot5}=5.99\\
&=\sqrt{\frac{2.42}{2}} + \sqrt{\frac{14.4}{2}}\\
&=\sqrt{\frac{121}{100}} + \sqrt{\frac{720}{100}}\\
&=\frac{11}{10} + \frac{12\sqrt5}{10}\\
&=1.1 + 1.2\sqrt5\\
\end{align*}$$
Which is correct. \(\left[1.1+1.2\sqrt5\right]^2=8.41+2.64\sqrt5\)