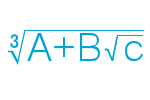
I have recently came across a problem involving cube roots of numbers added to square roots, in the form of \(\sqrt[3]{X+Y\sqrt{Z}}\), this is called a “nested radical.” I already figured out a nested square root, I decided to give this a go.
I can take a number like \((1+\sqrt5)^2\) and work out it is equal to \(16 + 8\sqrt5\). Unfortunately, it is very difficult to recognize that \(1+\sqrt5\) is the cube root (or even a factor) of that. Even harder, trying to find an equation such as \(\sqrt[3]{1080-624\sqrt3}\).
Recently, I developed a method of breaking down the equation into its cube root equation.
With an equation in the form of \(\sqrt[3]{X+Y\sqrt{Z}}\), where Z contains no perfect square factors.
Let’s start with
$$\begin{align} \sqrt[3]{X+Y\sqrt{Z}} &= A+B\sqrt{Z} \\
X+Y\sqrt{Z} &= (A+B\sqrt{Z})^3 \\
&=A^3 + 3A^2B\sqrt{Z} + 3AB^2Z + B^3Z\sqrt{Z} \\
&=A^3 + 3AB^2Z + 3A^2B\sqrt{Z} + B^3Z\sqrt{Z} \\
&=\color{Yellow}{A^3 + 3AB^2Z} +\color{cyan}{( 3A^2B + B^3Z})\sqrt{Z} .\\
\end{align}$$
We need to find
$$\begin{align} X &= \color{Yellow}{A^3 + 3AB^2Z} \tag{1}\label{1} \\
Y &=\color{cyan}{3A^2B + B^3Z}. \tag{2}\label{2}\\
\end{align}$$
If You look at X, You see it is the sum of a cube and a multiple of 3Z.
Let’s look at an example, \(\sqrt[3]{1080-624\sqrt{3}}\). If we subtract cubes from the initial number(1080) we get:
$$\begin{align} 1080-1^3 &= 1080-1= 1079 &\color{red}{No} \\
1080-2^3 &= 1080-8= 1072 &\color{red}{No}\\
1080-3^3 &= 1080-27=1053=3Z\cdot 117 &\color{lime}{Yes} \\
1080-4^3 &= 1080-64=1016 &\color{red}{No}\\
1080-5^3 &= 1080-125=955 &\color{red}{No}\\
1080-6^3 &= 1080-216=864=3Z\cdot 96 &\color{lime}{Yes} \\
1080-7^3 &= 1080-343=737 &\color{red}{No}\\
1080-8^3 &= 1080-512=568 &\color{red}{No}\\
1080-9^3 &= 1080-729=351=3Z\cdot 39 &\color{lime}{Yes} \\
1080-10^3 &= 1080-1000=80 &\color{red}{No}\\
1080-11^3 &= 1080-1331=-251 &\color{red}{No}\\
\end{align}$$
We need a result that is evenly divisible by 3Z, or 9 in this case. \(11^3\) is greater than 1080, so we stop. (Even if all answers are complex, B² will still be Real.)
Our results show 3, 6, and 9 are viable solutions for a, we must now check each against X to get B.
| if(A=3) | \(1053 =9\cdot 3\cdot B^2\) | B²=39 | \(B=\sqrt{39}\) |
| if(A=6) | \( 864 =9\cdot 6\cdot B^2\) | B²=16 | \(B=4\) |
| if(A=9) | \( 351 =9\cdot 9\cdot B^2\) | \(B^2=4\frac13\) | \(B=\sqrt{\frac{13}{3}}\) |
The only even square root is for A=6, B=4. \(X= 6^3 + 3\cdot6 \cdot 4^2 \cdot 3 =1080\), so this is a possible solution pair. First we must now check against Y.
$$\begin{align} Y &=3A^2B + B^3Z\\
&=3\cdot 6^2\cdot4 + 4^3\cdot3\\
&=3\cdot 36\cdot4 + 64\cdot3\\
&=432 + 192\\
&=624\\
\end{align}$$
It matches, so we have a correct solution for \(\sqrt[3]{1080-624\sqrt{3}} =6-4\sqrt{3} \). Remember, as the original had a negative Y, the solution must negate B.
If our example \(\sqrt[3]{1080-624\sqrt{3}}\) was actually \(\sqrt[3]{1080-623\sqrt{3}}\), then the formulas above would not work (there would not be any solution) and would not be able to be simplified any further.
Let’s try \(\sqrt[3]{\frac{371}{125}+\frac{319}{100}\sqrt2 }\), which can also be written \(\sqrt[3]{2.968+3.19\sqrt2 }\). This is a bit harder as we are not dealing with integers. It may be easier to try smaller cubes.
$$\begin{align} 2.968-.1^3 &= 2.968-.001= 2.967=3Z\cdot 0.4945 \\
2.968-.2^3 &= 2.968-.008= 2.960\\
2.968-.3^3 &= 2.968-.027= 2.941\\
2.968-.4^3 &= 2.968-.064= 2.904=3Z\cdot 0.4840\\
2.968-.5^3 &= 2.968-.125= 2.843\\
2.968-.6^3 &= 2.968-.216= 2.752\\
2.968-.7^3 &= 2.968-.343= 2.625=3Z\cdot 0.4375\\
2.968-.8^3 &= 2.968-.512= 2.456\\
2.968-.9^3 &= 2.968-.729= 2.239\\
2.968-1.0^3 &= 2.968-1.000= 1.968=3Z\cdot 0.328\\
2.968-1.1^3 &= 2.968-1.331= 1.637\\
2.968-1.2^3 &= 2.968-1.728= 1.240\\
2.968-1.3^3 &= 2.968-2.197= 0.771=3Z\cdot 0.1285\\
2.968-1.4^3 &= 2.968-2.744= 0.224\\
2.968-1.5^3 &= 2.968-3.375=-0.407 \\
\end{align}$$
Of these, 0.1, 0.4, 0.7, 1, and 1.3 are finitely divisible by 6 (3Z). If we didn’t find any, we would have to try smaller numbers.
| if (A=0.1) | \(2.967=6\cdot 0.1\cdot B^2\) | \(B^2=\frac{4945}{1000}\) | B is irrational |
| if (A=0.4) | \(2.904=6\cdot 0.4\cdot B^2\) | \(B^2=\frac{121}{100}\) | \(B=\frac{11}{10}\) |
| if (A=0.7) | \(2.625=6\cdot 0.7\cdot B^2\) | \(B^2=\frac58\) | \(B=\sqrt{\frac58}\) |
| if (A=1) | \(1.968=6\cdot 1\cdot B^2\) | \(B^2=\frac{41}{125}\) | B is irrational |
| if (A=1.3) | \(0.771=6\cdot 1.3\cdot B^2\) | \(B^2=\frac{257}{2600}\) | B is irrational |
Three of these are obviously irrational, so cannot be part of our solution, so are not calculated.
For A=0.7, B is also irrational, so we will first test A=0.4:
$$\begin{align} 2.968 &= A^3 + 3AB^2Z\\
&=0.4^3 +3\cdot 0.4\cdot B^2\cdot 2\\
&=0.064 + 2.4\cdot B^2\\
2.904&=2.4B^2\\
1.21&=B^2\\
B&=\frac{11}{10}=1.1\\
\end{align}$$
And for Y:
$$\begin{align} Y &=3A^2B + B^3Z\\
&=3\cdot 0.4^2\cdot1.1 + 1.1^3\cdot2\\
&=3\cdot 0.16\cdot1.1 + 1.331\cdot2\\
&=0.528 + 2.662\\
&=3.19\\
\end{align}$$
It matches, so we have a correct solution for \(\sqrt[3]{2.968+3.19\sqrt2 } =0.4+1.1\sqrt{2} \).
Any cube root in this form must also have \(X^2+Y^2\cdot Z\) equal a perfect cube.
\(\sqrt[3]{1080^2-624^2\cdot 3}= -12\) and \( \sqrt[3]{\frac{371}{125}^2-\frac{319}{100}^2\cdot2}=\frac{-113}{50} \), so these are solvable.
Also, remember that these are cube roots, so there are two complex roots. Just rotate the answer found by 120° and 240°, for the remaining answers. If this technique doesn’t find a simple answer, then all 3 may be complex.
Another way to solve, if Z=5 and the number under the radical is in the form of \(2K\pm K\sqrt5\), aka \(K\cdot(2\pm \sqrt5)\), the answer will be in the form of \(A\pm +A\sqrt5\). In this case, \(A=\sqrt[3]{\frac{K}{8}}\).
Alternate values for Z:
| Z | Form | A= |
| 2 | \(K(7\pm 5\sqrt2)\) | \(\sqrt[3]{K}\) |
| 3 | \(K(5\pm 3\sqrt3)\) | \(\sqrt[3]{\frac{K}{2}}\) |
| 5 | \(K(2\pm \sqrt5)\) | \(\sqrt[3]{\frac{K}{8}}\) |
| 6 | \(K(19\pm 9\sqrt6)\) | \(\sqrt[3]{K}\) |
| 7 | \(K(11\pm 5\sqrt7)\) | \(\sqrt[3]{\frac{K}{2}}\) |
| 8 | \(K(25\pm 11\sqrt8)\) or \(K(25\pm 22\sqrt2)\) | \(\sqrt[3]{K}\) |
| 10 | \(K(31\pm 13\sqrt{10})\) | \(\sqrt[3]{K}\) |
This is likely not the best method for finding the cube roots, but it does work.