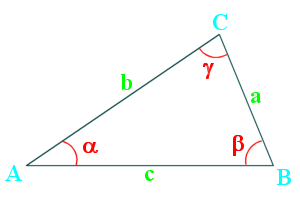
 The law of cosines relates the sides and angles of a triangle.
The law of cosines relates the sides and angles of a triangle.
\(a^2=b^2+c^2-2bc\cdot \cos\alpha \\ b^2=a^2+c^2-2ac\cdot \cos\beta \\ c^2=a^2+b^2-2ab\cdot \cos\gamma\)
It can also be rearranged to:
\(\large\alpha=\arccos\left(\frac{b^2+c^2-a^2}{2bc}\right) \\ \large\beta=\arccos\left(\frac{a^2+c^2-b^2}{2ac}\right) \\ \large\gamma=\arccos\left(\frac{a^2+b^2-c^2}{2ab}\right)\)
As long as all three sides or at least one side and two angles (which the third is trivial to find) are known, the remaining angles and sides are obtainable.
You can also use the law of sines, \(\Large\frac{a}{sin\alpha}=\frac{b}{sin\beta}=\frac{c}{sin\gamma}\) or \(\Large\frac{sin\alpha}{a}=\frac{sin\beta}{b}=\frac{sin\gamma}{c}\), although I prefer the former as sin90°=1, therefore eliminating it in the fraction.
Beware of ambiguous cases, such as if ∠α is acute and length a is shorter than b, then the ∠β can be acute or obtuse. Law of sines would give \(\large\beta=arcsin\frac{b\cdot sin\alpha}{a}\) or \(\large\beta=180-arcsin\frac{b\cdot sin\alpha}{a}\). Use the law of cosines in this case.
Always double check your work by using the opposite law to verify your findings.