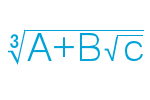Tag: nested radical

Nested roots, part 2

Webmaster SteveLeave a comment

I have recently came across a problem involving cube roots of numbers added to square roots, in the form of \(\sqrt[3]{X+Y\sqrt{Z}}\), this is called a “nested radical.” I already figured out a nested square root, I decided to give this a go.

I can take a number like \((1+\sqrt5)^2\) and work out it is equal to \(16 + 8\sqrt5\). Unfortunately, it is very difficult to recognize that \(1+\sqrt5\) is the cube root (or even a factor) of that. Even harder, trying to find an equation such as \(\sqrt[3]{1080-624\sqrt3}\).

Recently, I developed a method of breaking down the equation into its cube root equation.

With an equation in the form of \(\sqrt[3]{X+Y\sqrt{Z}}\), where Z contains no perfect square factors.

Let’s start with
$$\begin{align} \sqrt[3]{X+Y\sqrt{Z}} &= A+B\sqrt{Z} \\
X+Y\sqrt{Z} &= (A+B\sqrt{Z})^3 \\
&=A^3 + 3A^2B\sqrt{Z} + 3AB^2Z + B^3Z\sqrt{Z} \\
&=A^3 + 3AB^2Z + 3A^2B\sqrt{Z} + B^3Z\sqrt{Z} \\
&=\color{Yellow}{A^3 + 3AB^2Z} +\color{cyan}{( 3A^2B + B^3Z})\sqrt{Z} .\\
\end{align}$$

We need to find
$$\begin{align} X &= \color{Yellow}{A^3 + 3AB^2Z} \tag{1}\label{1} \\
Y &=\color{cyan}{3A^2B + B^3Z}. \tag{2}\label{2}\\
\end{align}$$

If You look at X, You see it is the sum of a cube and a multiple of 3Z.

Let’s look at an example, \(\sqrt[3]{1080-624\sqrt{3}}\). If we subtract cubes from the initial number(1080) we get:

$$\begin{align} 1080-1^3 &= 1080-1= 1079  &\color{red}{No} \\
1080-2^3 &= 1080-8= 1072  &\color{red}{No}\\
1080-3^3 &= 1080-27=1053=3Z\cdot 117  &\color{lime}{Yes}  \\
1080-4^3 &= 1080-64=1016  &\color{red}{No}\\
1080-5^3 &= 1080-125=955  &\color{red}{No}\\
1080-6^3 &= 1080-216=864=3Z\cdot 96  &\color{lime}{Yes}  \\
1080-7^3 &= 1080-343=737  &\color{red}{No}\\
1080-8^3 &= 1080-512=568 &\color{red}{No}\\
1080-9^3 &= 1080-729=351=3Z\cdot 39  &\color{lime}{Yes}  \\
1080-10^3 &= 1080-1000=80  &\color{red}{No}\\
1080-11^3 &= 1080-1331=-251 &\color{red}{No}\\
\end{align}$$

We need a result that is evenly divisible by 3Z, or 9 in this case. \(11^3\) is greater than 1080, so we stop. (Even if all answers are complex, B² will still be Real.)

Our results show 3, 6, and 9 are viable solutions for a, we must now check each against X to get B.

if(A=3) \(1053 =9\cdot 3\cdot B^2\) B²=39 \(B=\sqrt{39}\)
if(A=6) \( 864 =9\cdot 6\cdot B^2\) B²=16 \(B=4\)
if(A=9) \( 351 =9\cdot 9\cdot B^2\) \(B^2=4\frac13\) \(B=\sqrt{\frac{13}{3}}\)

The only even square root is for A=6, B=4. \(X= 6^3 + 3\cdot6 \cdot 4^2 \cdot 3 =1080\), so this is a possible solution pair. First we must now check against Y.

$$\begin{align} Y &=3A^2B + B^3Z\\
&=3\cdot 6^2\cdot4 + 4^3\cdot3\\
&=3\cdot 36\cdot4 + 64\cdot3\\
&=432 + 192\\
&=624\\
\end{align}$$

It matches, so we have a correct solution for \(\sqrt[3]{1080-624\sqrt{3}} =6-4\sqrt{3} \). Remember, as the original had a negative Y, the solution must negate B.

If our example \(\sqrt[3]{1080-624\sqrt{3}}\) was actually \(\sqrt[3]{1080-623\sqrt{3}}\), then the formulas above would not work (there would not be any solution) and would not be able to be simplified any further.

 

Let’s try \(\sqrt[3]{\frac{371}{125}+\frac{319}{100}\sqrt2 }\), which can also be written \(\sqrt[3]{2.968+3.19\sqrt2 }\). This is a bit harder as we are not dealing with integers. It may be easier to try smaller cubes.

$$\begin{align} 2.968-.1^3 &= 2.968-.001= 2.967=3Z\cdot 0.4945 \\
2.968-.2^3 &= 2.968-.008= 2.960\\
2.968-.3^3 &= 2.968-.027= 2.941\\
2.968-.4^3 &= 2.968-.064= 2.904=3Z\cdot 0.4840\\
2.968-.5^3 &= 2.968-.125= 2.843\\
2.968-.6^3 &= 2.968-.216= 2.752\\
2.968-.7^3 &= 2.968-.343= 2.625=3Z\cdot 0.4375\\
2.968-.8^3 &= 2.968-.512= 2.456\\
2.968-.9^3 &= 2.968-.729= 2.239\\
2.968-1.0^3 &= 2.968-1.000= 1.968=3Z\cdot 0.328\\
2.968-1.1^3 &= 2.968-1.331= 1.637\\
2.968-1.2^3 &= 2.968-1.728= 1.240\\
2.968-1.3^3 &= 2.968-2.197= 0.771=3Z\cdot 0.1285\\
2.968-1.4^3 &= 2.968-2.744= 0.224\\
2.968-1.5^3 &= 2.968-3.375=-0.407 \\
\end{align}$$

Of these, 0.1, 0.4, 0.7, 1, and 1.3 are finitely divisible by 6 (3Z). If we didn’t find any, we would have to try smaller numbers.

if (A=0.1) \(2.967=6\cdot 0.1\cdot B^2\) \(B^2=\frac{4945}{1000}\) B is irrational
if (A=0.4) \(2.904=6\cdot 0.4\cdot B^2\) \(B^2=\frac{121}{100}\) \(B=\frac{11}{10}\)
if (A=0.7) \(2.625=6\cdot 0.7\cdot B^2\) \(B^2=\frac58\) \(B=\sqrt{\frac58}\)
if (A=1) \(1.968=6\cdot 1\cdot B^2\) \(B^2=\frac{41}{125}\) B is irrational
if (A=1.3) \(0.771=6\cdot 1.3\cdot B^2\) \(B^2=\frac{257}{2600}\) B is irrational

Three of these are obviously irrational, so cannot be part of our solution, so are not calculated.

For A=0.7, B is also irrational, so we will first test A=0.4:

$$\begin{align} 2.968 &= A^3 + 3AB^2Z\\
&=0.4^3 +3\cdot 0.4\cdot B^2\cdot 2\\
&=0.064 + 2.4\cdot B^2\\
2.904&=2.4B^2\\
1.21&=B^2\\
B&=\frac{11}{10}=1.1\\
\end{align}$$

And for Y:

$$\begin{align} Y &=3A^2B + B^3Z\\
&=3\cdot 0.4^2\cdot1.1 + 1.1^3\cdot2\\
&=3\cdot 0.16\cdot1.1 + 1.331\cdot2\\
&=0.528 + 2.662\\
&=3.19\\
\end{align}$$

It matches, so we have a correct solution for \(\sqrt[3]{2.968+3.19\sqrt2 } =0.4+1.1\sqrt{2} \).

Any cube root in this form must also have \(X^2+Y^2\cdot Z\) equal a perfect cube.

\(\sqrt[3]{1080^2-624^2\cdot 3}= -12\) and \( \sqrt[3]{\frac{371}{125}^2-\frac{319}{100}^2\cdot2}=\frac{-113}{50} \), so these are solvable.

Also, remember that these are cube roots, so there are two complex roots. Just rotate the answer found by 120° and 240°, for the remaining answers. If this technique doesn’t find a simple answer, then all 3 may be complex.

Another way to solve, if Z=5 and the number under the radical is in the form of \(2K\pm K\sqrt5\), aka \(K\cdot(2\pm \sqrt5)\), the answer will be in the form of \(A\pm +A\sqrt5\). In this case, \(A=\sqrt[3]{\frac{K}{8}}\).

Alternate values for Z:

Z Form A=
2 \(K(7\pm 5\sqrt2)\) \(\sqrt[3]{K}\)
3 \(K(5\pm 3\sqrt3)\) \(\sqrt[3]{\frac{K}{2}}\)
5 \(K(2\pm \sqrt5)\) \(\sqrt[3]{\frac{K}{8}}\)
6 \(K(19\pm 9\sqrt6)\) \(\sqrt[3]{K}\)
7 \(K(11\pm 5\sqrt7)\) \(\sqrt[3]{\frac{K}{2}}\)
8 \(K(25\pm 11\sqrt8)\) or \(K(25\pm 22\sqrt2)\) \(\sqrt[3]{K}\)
10 \(K(31\pm 13\sqrt{10})\) \(\sqrt[3]{K}\)

This is likely not the best method for finding the cube roots, but it does work.

 

Factoring numbers with square root terms

Webmaster SteveLeave a comment

Quite often, when doing calculations on polyhedra, you will find yourself with complex equations like \(\frac{20+7\sqrt3}{1+2\sqrt3}\).

Is the top evenly divisible by the bottom? I certainly can’t tell just by looking at them.

There must be a method to factor the numerator.

Quite often, when doing calculations on polyhedra, you will find yourself with complex equations like $$\begin{equation}\tag{eq1}\label{eq1}\frac{20+7\sqrt3}{1+2\sqrt3}\end{equation}$$

Is the top evenly divisible by the bottom? I certainly can’t tell just by looking at them.

There must be a method to factor the numerator.

Let’s start with $$\color{blue}{(A+B\sqrt{R})}\color{lime}{(C+D\sqrt{R})}$$ multiplying the terms together gives $$\color{salmon}{AC+BRD+(BC+AD)\sqrt{R}}$$

So, $$\frac{\color{salmon}{AC+BRD+(BC+AD)\sqrt{R}}}{\color{blue}{A+B\sqrt{R}}} = \color{lime}{C+D\sqrt{R}}$$

Then we can substitute known values (A=1, B=2, R=3) into the formula. $$\frac{1C+2(3)D+(2C+1D)\sqrt{3}}{1+2\sqrt{3}} = C+D\sqrt{3}$$

Finding the answer is just a matter of finding C and D.

Consider that
$$\frac{\color{yellow}{C+6D} + \color{cyan}{(2C+D)}\sqrt3}{1+2\sqrt3} = \frac{\color{yellow}{20}+\color{cyan}{7}\sqrt3}{1+2\sqrt3}$$

We can break the equation into the colored sections to find $$\begin{align}\color{yellow}{C+6D} & \color{yellow}{=20} \\ C&=20-6D\tag{eq2}\label{eq2} \end{align}$$ and $$\color{cyan}{2C+D = 7}\tag{eq3}\label{eq3}$$

We now know C \eqref{eq2}, at least in terms of D, then substitute this into \eqref{eq3}.
$$\begin{align}2(20-6D)+D &= 7 \\ 40-12D+D &= 7 \\ -11D &= 7-40 = -33 \\D &= \frac{-33}{-11} \\ D&=3\end{align}$$

Returning to \eqref{eq2} and substituting D=3, we get \(C = 20-6\cdot 3 = 20-18 = 2\).

Then our answer should be \(2+3\sqrt{3}\), and it is, because \((1+2\sqrt3)(2+3\sqrt3) = 20+7\sqrt3\).

This method make it simple to divide out these complicated numbers, although, you might not get a simpler answer. For example, if we change \eqref{eq1} to \(\Large\frac{19+7\sqrt3}{1+2\sqrt3}\), we end up with answers C=23/11 and D=31/11, but it still works as \((1+2\sqrt3)(\frac{23}{11}+\frac{31\sqrt3}{11}) = 19+7\sqrt3\). Although, we could write our answer as \(\frac{1}{11}(23+31\sqrt3)\).

Another example:$$\frac{-3}{3+2\sqrt3}$$
We have values (A=3, B=2, R=3), giving $$3C + 2\cdot3D + (2C+3D)\sqrt3 = (3+2\sqrt3)(C+D\sqrt3)$$

Remember that \(-3\) is the same as \(-3+0\sqrt3\). So
$$\begin{align}3C+6D&=-3\label{e2}\tag{eq4}\\
2C+3D&=0\label{e3}\tag{eq5}
\end{align}$$

Working out \eqref{e2} gives
$$\begin{align}3C+6D&=-3 \\ 6D&= -3-3C \\D&=\frac{3(-1-C)}{6} \\D&= \frac{-1-C}{2}\end{align}$$

Plugging into \eqref{e3}, gives
$$\begin{align}2C+3D&=0 \\ 2C+3\cdot(\frac{-1-C}{2})&=0 \\ \frac{4C}{2}+\frac{-3C-3}{2}&=0 \\ \frac{4C-3C-3}{2}&=0 \\ \frac{C-3}{2}&=0 \\ C-3&=0 \\C&=3\end{align}$$

With C=3, we can find D in \eqref{e2} $$\begin{align}3(3)+6D&=-3 \\ 9+6D&=-3 \\ 6D&=-3-9 \\ 6D&=-12 \\ D&=\frac{-12}{6} \\ D&=-2\end{align}$$

So the answer is \(3-2\sqrt3\), as \((3+2\sqrt3)(3-2\sqrt3)=-3\).

You might notice this is the same as the “Difference of 2 squares” (x-y)(x+y) = x²-xy+xy-y² = x²-y². The “xy” terms cancel each other out, leaving 0. (x-y) and (x+y) are conjugates of one another, so when you have a numerator with a zero times the square root (or in other words, the numerator is a whole number), you may wish to try the denominator’s conjugate first. It may not be the answer you seek, but it can help you sometimes.

If the denominator is a whole number (or rational), $$\frac{6+2\sqrt3}{-2}$$

then divide both parts of the numerator by the denominator,

$$\frac{6}{-2}+\frac{2\sqrt3}{-2}=-3-\sqrt3$$

So to find an answer to $$\notag\frac{X+Y\sqrt{R}}{A+B\sqrt{R}} = C+D\sqrt{R}$$

You will need to find the solutions to \(AC+BRD=X\) and \(BC+AD=Y\)

UPDATE: I have also realized that you can just multiply the top and bottom of the fraction by the denominator’s conjugate.

In the first equation:

$$\begin{align}\frac{20+7\sqrt3}{1+2\sqrt3}&=\frac{(20+7\sqrt3)(1-2\sqrt3)}{(1+2\sqrt3)(1-2\sqrt3)}\\&=\frac{20-42+7\sqrt3-40\sqrt3}{1-12}\\&=\frac{-22-33\sqrt3}{-11}\\&=2+3\sqrt3\end{align}$$

In this method, the denominator is always a whole number (if both A&B are whole numbers).

sqr(A+B*sqr(C))

Webmaster SteveLeave a comment

Lately, I have been doing a lot of math involving square roots of numbers added to square roots, in the form of \(\sqrt{A+B\sqrt{C}}\), this is called a “nested radical.” Normally, you would not be able to simplify any further, unless there was a common factor of both that could be removed, or if both items had the same number under the radical (eg. \(\sqrt{4\sqrt7+12\sqrt7}=\sqrt{16\sqrt7}=4\sqrt[4]{7}\) ).

I can take a number like \((1+\sqrt5)^2\) and work out it is equal to \(6 + 2\sqrt5\). Unfortunately, it is very difficult to recognize that \(1+\sqrt5\) is the square root (or even a factor) of that. Even harder, trying to find an equation such as \(\sqrt{469+144\sqrt5}\).

Recently, I found a method of breaking down the equation into its square root equation.

With an equation in the form of \(\sqrt{A+B\sqrt{C}}\), where C contains no perfect square factors, taking the formula \(D^2 = A^2 – (B^2)*C\), if D is a rational number, you will be able to factor the equation, otherwise it is simplified as much as is possible.

Then you will be able to get the formula: \(\sqrt{A+B\sqrt{C}} = \pm \left(\sqrt{\frac{A-D}{2}} + sign(A*B)*\sqrt{\frac{A+D}{2}}\right)\), where sign(A*B) is the positive or negative value of A*B, it will always give you 0, +1, or -1.

So to find \(\sqrt{469+144\sqrt5}\), we find \(469^2 – 144^2 * 5 = 116281\). Since 116281 = 341*341, we can plug D=341 into the formula to get:

$$\begin{align} \sqrt{\frac{469-341}{2}} + 1*\sqrt{\frac{469+341}{2}}&=\sqrt{\frac{128}{2}} + \sqrt{\frac{810}{2}}\\
&=\sqrt{64} + \sqrt{405} \\
&= 8 + \sqrt{81*5} \\
&= 8+9\sqrt{5}\end{align}$$

So, \(\sqrt{469+144\sqrt5} = (8+9\sqrt{5}) \text{ and } (-8-9\sqrt{5})\).

To find \(\sqrt{53-12\sqrt{11}}\), we find \(53^2 – 12^2 * 11 = 1225\). Since 1225 = 35*35, we can plug D=35 into the formula to get:

$$\begin{align*} \sqrt{\frac{53-35}{2}} + -1*\sqrt{\frac{53+35}{2}} &=\sqrt{\frac{18}{2}} – \sqrt{\frac{88}{2}}\\
&=\sqrt{9} – \sqrt{44} \\
&= 3 – \sqrt{4*11} \\
&= 3-2\sqrt{11} \end{align*}$$

So, \(\sqrt{53-12\sqrt11} = (3-2\sqrt{11}) \text{ and } (-3+2\sqrt{11})\).

If A and B have the same sign, the answer will have both terms the same sign ({+,+} and {-,-} are equally valid). If A and B have different signs, the terms in the answer will have different signs ({+,-} and {-,+}). Often you will need to determine the complete answer that equates to positive, after all, it is hard to have a real object with a negative length.

An interesting correlation: \((X-Y)^2 = (Y-X)^2\), but remember \(\sqrt{X-Y} \not= \sqrt{Y-X}\). Double check your signs by re-squaring your answer.

Note: This still works if D is not an integer, but is rational:

$$\begin{align*} \sqrt{8.41+2.64\sqrt5} &=\sqrt{\frac{8.41-5.99}{2}} + \sqrt{\frac{8.41+5.99}{2}} &D=\sqrt{8.41^2 + 2.64^2\cdot5}=5.99\\
&=\sqrt{\frac{2.42}{2}} + \sqrt{\frac{14.4}{2}}\\
&=\sqrt{\frac{121}{100}} + \sqrt{\frac{720}{100}}\\
&=\frac{11}{10} + \frac{12\sqrt5}{10}\\
&=1.1 + 1.2\sqrt5\\
\end{align*}$$

Which is correct. \(\left[1.1+1.2\sqrt5\right]^2=8.41+2.64\sqrt5\)