
The cube is probably the most recognized and best known of and 3D shape. Kids young enough not to even know how to talk will still know about cubes, they play with multicolored wooden blocks. Older kids may tackle the Rubik’s Cube puzzle or play Yahtzee with dice. Then they may graduate to working in a cubicle as adults.
We use the cube as a representation of the space around us. Pepsi was briefly sold in 24-can “cubes.” Apple’s G4 computer was cubic.
Al Kaaba (literal English, the cube) is a cuboid shaped building in Mecca and the most sacred site to Islam.
Salt grows into cubic crystals.
Stones chipped and shaped into cubes have been found that date back 100’s of thousands of years.
Star Trek’s fictional, I hope, Borg traveled through space in a cube shaped ship.
There are several prisons with the nickname “the cube,” despite not having walls as tall as they are wide.
They are literally, all around us. We have have such a familiarity with the cube that we don’t even have to think about its qualities or structure. We just know it.
Therefore, having a page devoted to the cube may seem like a waste of space, but I’m certain that there is still knowledge we can gain from re-examining the world around us.
 The cube is a 3 dimensional solid object made of 6 squares (variously called faces, facets, or sides), each meeting at right (90°) angles with two others. It is one of the 5 Platonic solids and can also be referred to as a regular hexahedron or a square prism.
The cube is a 3 dimensional solid object made of 6 squares (variously called faces, facets, or sides), each meeting at right (90°) angles with two others. It is one of the 5 Platonic solids and can also be referred to as a regular hexahedron or a square prism.
Like a sphere is the set of all points equidistant from the origin, the cube is the set of points that make up the square faces, it has no volume, although we usually refer to the volume it contains.
If we call the edge length S, then each face will have area \(S^2\), so the cube will have surface area \(6*S^2\). The internal volume is \(S^3\).
Many different shapes can tile 2D space, squares, hexagons, various triangles. The cube is the only object that can regularly tile Euclidean 3D space.
Using formulas already mentioned, vertex edge angles are: \(\Large\cos\mu=\frac{cos90}{cos45}=\frac{0}{\frac{1}{\sqrt2}}=0, \mu=90^\circ\).
Using a cube with vertexes named A-H, as in the image, with edge length of 1, we can then calculate other lengths, easily done with right triangles and the Pythagorean theorem. Actually, it is even easier as almost all will be 45° right triangles.
Drawing a diagonal across a face from B to D, we get a right triangle with BD length \(\sqrt2\). Drawing diagonal AC crosses at the midpoint J.
Drawing a spacial diagonal through the cube from A to G, triangle AEG lengths would be \(1,\sqrt2, and \sqrt3\). Midpoint of AG is K which is also the spacial midpoint of the cube. AK and GK are \(\frac{\sqrt3}{2}\), the radius of a sphere surrounding the cube.
 To find JK:
To find JK:
$$\begin{align}
(AJ)^2+(JK)^2&=(AK)^2\\
(JK)^2&=(AK)^2-(AJ)^2\\
&=\left(\frac{\sqrt3}{2}\right)^2-\left(\frac{\sqrt2}{2}\right)^2\\
&=\frac34-\frac24\\
&=\frac14\\
JK&=\frac12\end{align}$$ so JK=\(\frac12\). This is the radius of an inscribed sphere.
The midpoint of CD is L. Line JL would 1/2 the edge length, equal to JK, so \(KL=\frac{\sqrt2}{2}=\frac1{\sqrt2}\). Angle JLK is 45°, one half the dihedral (face to face) angle.
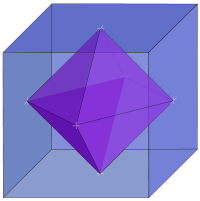
If you join the mid-face points (all the J’s), you would then get the cube’s dual shape called the octahedron. Similarly, joining the midpoints of the octahedron’s face would give you a cube. An octahedron inside a cube of edge length S would have edges of length \(S\cdot\frac1{\sqrt2}\) and an octahedron outside the cube would have edge length of \(S\cdot\sqrt2\). The octahedra would have volumes of \(S^3\cdot\frac13\) and \(S^3\cdot\frac23\), respective.