Tag: Platonic solid

Octahedron

Webmaster SteveLeave a comment

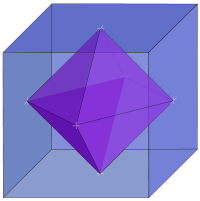
The octahedron is a Platonic solid, which means it is made of all regular polygons for each face, being eight equilateral triangles arranged four at each vertex.

With edge length of S, the surface area would be that of 8 equilateral triangles, \(8\cdot S^2\cdot \frac{\sqrt3}{4}=2\cdot S^2\sqrt3\).

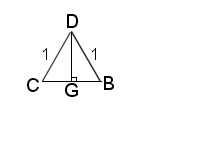
If we slice one in half, through 4 co-planar vertices, we get two 4-sided pyramids. Since we know that all the edges are the same length and all the angles are the same, the only possible shape for the base would have to be a square.

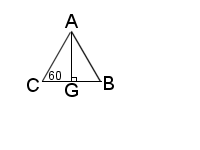
If there were only three triangles meeting at the apex, instead of four, we could use the formula found earlier to get the vertex edge angle, but we don’t need to recalculate a new formula. Slicing through any co-planar vertices will result in a square-based pyramid. Therefore, at each vertex, each edge is 60° to the ones on either side of it and 90° to the fourth.

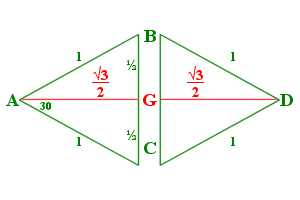
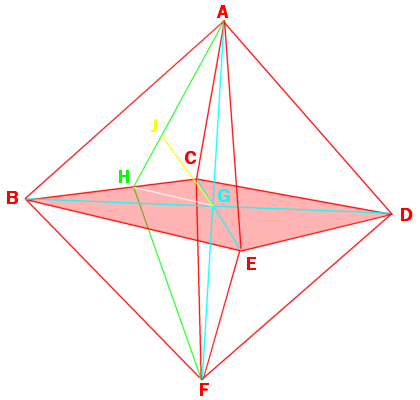
Given an octahedron with edge length of 1 and vertices A-F, we can draw diagonals (AF, BD, CE) across opposite corners, each being the same length \(\sqrt2\), and meeting at point G, the center of the octahedron. Half of these lengths is \(\frac{\sqrt2}{2} \text{, or } \frac{1}{\sqrt2}\), which is the radius of the circumscribed sphere.

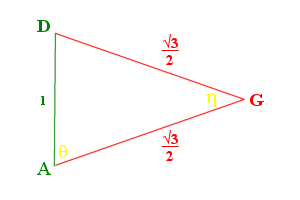
The midpoint of line BC is H. Line AH and FH are length \(\frac{\sqrt3}{2}\). We now have a triangle AHF. We then can use the law of cosines to find ∠AHF,

$$\begin{align}\cos\angle AHF &=\frac{(AH)^2+(FH)^2-(AF)^2}{2(AH)(AF)}\\ &=\frac{\left(\frac{\sqrt3}{2}\right)^2+\left(\frac{\sqrt3}{2}\right)^2 – \sqrt2^2}{2\cdot\frac{\sqrt3}{2}\cdot\frac{\sqrt3}{2}} \\ &=\frac{\frac34+\frac34-2}{\frac32}\\ &=\left(\frac64-\frac84\right)\cdot\frac23 \\ &= -\frac24\cdot\frac23 \\ &= -\frac{4}{12}\\ &=-\frac13\end{align}$$

So \(\cos\angle AHF =-\frac13\), ∠AHF= 109.4712206…°, the dihedral angle.

Placing point J at the circumcenter of ΔABC, gives a line AJ of length \(\sqrt{\frac13}\), and ∠AJG is 90°. Solving for GJ gives:

$$\begin{align}(GJ)^2+(AJ)^2&=(AG)^2\\(GJ)^2 + \left(\frac{1}{\sqrt3}\right)^2 &= \left(\frac{1}{\sqrt2}\right)^2\\(GJ)^2 &= \left(\frac{1}{\sqrt2}\right)^2-\left(\frac{1}{\sqrt3}\right)^2\\(GJ)^2 &= \frac12-\frac13\\ &=\frac16 \end{align}$$

\(GJ=\sqrt\frac16\), the radius of an inscribed sphere.

Joining the centers of each triangle, gives the edges a cube, the dual of the octahedron.

The Cube

Webmaster SteveLeave a comment

The cube is probably the most recognized and best known of and 3D shape. Kids young enough not to even know how to talk will still know about cubes, they play with multicolored wooden blocks. Older kids may tackle the Rubik’s Cube puzzle or play Yahtzee with dice. Then they may graduate to working in a cubicle as adults.

We use the cube as a representation of the space around us. Pepsi was briefly sold in 24-can “cubes.” Apple’s G4 computer was cubic.

Al Kaaba (literal English, the cube) is a cuboid shaped building in Mecca and the most sacred site to Islam.

Salt grows into cubic crystals.

Stones chipped and shaped into cubes have been found that date back 100’s of thousands of years.

Star Trek’s fictional, I hope, Borg traveled through space in a cube shaped ship.

There are several prisons with the nickname “the cube,” despite not having walls as tall as they are wide.

They are literally, all around us. We have have such a familiarity with the cube that we don’t even have to think about its qualities or structure. We just know it.

Therefore, having a page devoted to the cube may seem like a waste of space, but I’m certain that there is still knowledge we can gain from re-examining the world around us.

The cube is a 3 dimensional solid object made of 6 squares (variously called faces, facets, or sides), each meeting at right (90°) angles with two others. It is one of the 5 Platonic solids and can also be referred to as a regular hexahedron or a square prism.

Like a sphere is the set of all points equidistant from the origin, the cube is the set of points that make up the square faces, it has no volume, although we usually refer to the volume it contains.

If we call the edge length S, then  each face will have area \(S^2\), so the cube will have surface area \(6*S^2\). The internal volume is \(S^3\).

Many different shapes can tile 2D space, squares, hexagons, various triangles. The cube is the only object that can regularly tile Euclidean 3D space.

Using formulas already mentioned, vertex edge angles are: \(\Large\cos\mu=\frac{cos90}{cos45}=\frac{0}{\frac{1}{\sqrt2}}=0, \mu=90^\circ\).

Using a cube with vertexes named A-H, as in the image, with edge length of 1, we can then calculate other lengths, easily done with right triangles and the Pythagorean theorem. Actually, it is even easier as almost all will be 45° right triangles.

Drawing a diagonal across a face from B to D, we get a right triangle with BD length \(\sqrt2\). Drawing diagonal AC crosses at the midpoint J.

Drawing a spacial diagonal through the cube from A to G, triangle AEG lengths would be \(1,\sqrt2, and \sqrt3\). Midpoint of AG is K which is also the spacial midpoint of the cube. AK and GK are \(\frac{\sqrt3}{2}\), the radius of a sphere surrounding the cube.

To find JK:
$$\begin{align}
(AJ)^2+(JK)^2&=(AK)^2\\
(JK)^2&=(AK)^2-(AJ)^2\\
&=\left(\frac{\sqrt3}{2}\right)^2-\left(\frac{\sqrt2}{2}\right)^2\\
&=\frac34-\frac24\\
&=\frac14\\
JK&=\frac12\end{align}$$ so JK=\(\frac12\). This is the radius of an inscribed sphere.

The midpoint of CD is L. Line JL would 1/2 the edge length, equal to JK, so \(KL=\frac{\sqrt2}{2}=\frac1{\sqrt2}\). Angle JLK is 45°, one half the dihedral (face to face) angle.

If you join the mid-face points (all the J’s), you would then get the cube’s dual shape called the octahedron. Similarly, joining the midpoints of the octahedron’s face would give you a cube. An octahedron inside a cube of edge length S would have edges of length \(S\cdot\frac1{\sqrt2}\) and an octahedron outside the cube would have edge length of \(S\cdot\sqrt2\). The octahedra would have volumes of \(S^3\cdot\frac13\) and \(S^3\cdot\frac23\), respective.

Tetrahedron

Webmaster SteveLeave a comment

I started off posting about the truncated icosahedron, despite being fairly complex compared to the platonic solids, like the tetrahedron.

The regular tetrahedron is probably the simplest 3D shape, except for maybe the sphere. It is made of 4 equilateral triangles, forming a triangular pyramid.

Starting with a tetrahedron with vertexes named A, B, C, & D, with D as the apex (fig. 1), we can bisect ΔABC from point A to line BC and call that point G (fig. 2).


Figure 1
Figure 2
Figure 3

The bisection of ΔDBC would follow the same, a line DG would also equal AG. Figure 3 shows the cross section of the tetrahedron, ΔADG. We can then use the law of cosines to find ∠θ and ∠η.

\(\Large\cos \eta = \frac{AG^{2} + DG^{2} – AD^{2}}{2\cdot AG \cdot DG} = \frac{\frac34 + \frac34 – 1}{2\cdot\frac{\sqrt{3}}{2}\cdot\frac{\sqrt{3}}{2}} = \frac{\frac24}{\frac64} = \frac13\).

The angle (η) between each face, the dihedral angle, is \(cos^{-1} (\frac{1}{3})=70.528779\ldots^\circ\).

\(\Large\cos \theta = \frac{AG^{2} + AD^{2} – DG^{2}}{2\cdot AG \cdot AD} = \frac{\frac34 + 1 – \frac34}{2\cdot 1\cdot\frac{\sqrt{3}}{2}} = \frac{1}{\sqrt3}\).

The angle that the edge to face (θ) makes would be \(cos^{-1}\frac{1}{\sqrt{3}}= 54.73561\ldots^\circ\). Also since ΔADG is isosceles, ∠ADG = ∠DAG = θ.

\(2\cdot\theta+\eta=180^\circ\)

From the above equations and figures, you can then calculate other aspects, such as the height.

But what about non-regular tetrahedra? Let’s think about other pyramids, both fat and short and tall and thin. All the triangles in the regular tetrahedron have three 60° corners.

Let’s suppose that the angles originating at point D are all equal (we will call them λ), and the edges are also equal (we will call them length 1). We would have something like that of a camera tripod.

If we spread the legs, the camera will get lower to the ground and if we bring the legs together, the camera will get higher. The same is true of our pyramid.


Figure 4
Figure 5
Figure 6

Let us again bisect the angles λ, as shown in fig. 4.

\( BG = CG= \sin(\frac{\lambda}{2})\), \( BC= 2\cdot \sin(\frac{\lambda}{2})\), \( DG= \cos(\frac{\lambda}{2})\).

Looking at the pyramid’s base ΔABC (fig. 5), \(BC = AC= AB = 2\cdot \sin(\frac{\lambda}{2})\), then \(AG = BG\cdot\sqrt{3} = \sqrt{3}\cdot sin(\frac{\lambda}{2})\).

We again us the law of cosines to find μ (fig. 6).

\(\Large\cos\mu=\frac{1+cos^{2}\frac{\lambda}{2} – 3\cdot sin^{2}\frac{\lambda}{2}}{2\cdot cos\frac{\lambda}{2}}\)

If we add \((1\cdot sin^{2}\frac{\lambda}{2} -1\cdot sin^{2}\frac{\lambda}{2})\), which equals zero, to the top of the equation, we get \(\large\cos\mu=\frac{1+(cos^{2}\frac{\lambda}{2}) – 4\cdot sin^{2}\frac{\lambda}{2}+(sin^{2}\frac{\lambda}{2})}{2\cdot cos\frac{\lambda}{2}}\). Note the change of the three to four.

The items in parentheses can be combined using the identity cos² α + sin² α = 1:

\(\Large\cos\mu=\frac{1+1-4\cdot sin^{2}\frac{\lambda}{2}}{2\cdot cos\frac{\lambda}{2}}=\frac{2-4\cdot sin^{2}\frac{\lambda}{2}}{2\cdot cos\frac{\lambda}{2}}=\frac{1-2\cdot sin^{2}\frac{\lambda}{2}}{cos\frac{\lambda}{2}}\).

Using the identity cos 2α = 1 – 2·sin² α, gives: \(\large\cos\mu=\frac{cos\lambda}{cos\frac{\lambda}{2}}\).

We can then use this formula to verify the regular tetrahedron’s vertex edge angle that we found earlier. If \(\lambda=60^\circ\), \(\large\cos\mu=\frac{cos60}{cos30}=\frac{\frac12}{\frac{\sqrt{3}}{2}}=\frac{1}{\sqrt{3}}\), which is the same as θ above.

This formula can also be used on other polyhedra where there are three identical angles joining at a vertex, such as the cube,\(\large\cos\mu=\frac{cos90}{cos45}=\frac{0}{\frac{1}{\sqrt2}}=0, \mu=90^\circ\) or dodecahedron, \(\large\cos\mu=\frac{cos108}{cos54}=\frac{\frac{1-\sqrt5}{4}}{\frac{\sqrt{10-2\sqrt5}}{4}}=\frac{1-\sqrt5}{\sqrt{10-2\sqrt5}}, \mu=121.71747^\circ\).

I will get to the dodecahedron soon. The cube is so easy to figure out mathematically, rather boring.

Next posting, I will show you what happens if the pyramid leans a bit, that is if one of the apex angles is different that the other two.