Last post, I worked on the vertex edge angles of a triangular pyramid that had all equal angles originating from the apex.
Using the same camera tripod analogy, take one of the legs (line DA) of the tripod and slide it out further from the other two, but keep it equally distant from each. You now have a camera that’s about to crash to the floor, but you also have a pyramid that has two equal apex angles and that leans.
A right pyramid is a pyramid for which the apex lies directly above the centroid of the base. I don’t know if there is an actual name for a leaning pyramid, but I will just call it a leaning pyramid.
Again, we will work with a pyramid with vertexes A, B, C, & D, with D as the apex (Fig. 1). Again, the legs DA, DB, & DC are all equal length of 1 unit.
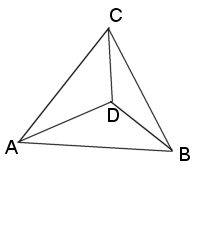 Figure 1 |
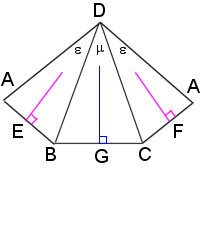 Figure 2 |
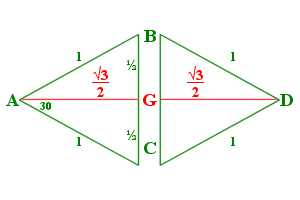
We can “unfold” the pyramid (Fig. 2) to show the bisection of the apex angles where they join the base vertexes, the midpoints E, F, & G.
We can see BG=CG, and AE=BE=CF=AF, and DE=DF.
Since ΔDAB = ΔDAC, we will ignore showing the the latter in the formulas. Both are isosceles, as well as ΔDBC.
\(\large{ BG=CG= sin(\frac{\mu}{2})\\
BC=2\cdot sin(\frac{\mu}{2})\\
DG=cos(\frac{\mu}{2})\\
AE=BE= sin(\frac{\epsilon}{2})\\
AB=2\cdot sin(\frac{\epsilon}{2})\\
DE=cos(\frac{\epsilon}{2})}\)
Items that must be true for this to be a real 3D object: \(2\cdot\epsilon>\mu, 2\cdot\epsilon+\mu<360^\circ\).
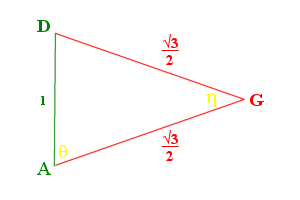
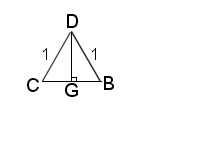
Figure 3 shows how to find the line AG on the base triangle. Using the Pythagorean theorem, \( AG=\sqrt{4\cdot sin^{2}(\epsilon/2)-sin^{2}(\mu/2)}\).
We split the pyramid in half, giving us cross section ΔADG (Fig. 4).
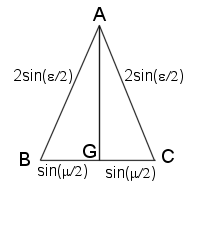 Figure 3 |
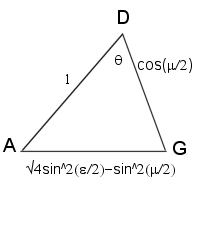 Figure 4 |
Using law of cosines, we get:
$$\large{\begin{align}\cos\theta
&=\frac{1^2+\cos^{2}(\frac{\mu}{2})-4\cdot \sin^{2}(\frac{\epsilon}{2})+\sin^{2}(\frac{\mu}{2})}{2\cdot 1\cdot \cos(\frac{\mu}{2})}\\
&=\frac{1 +[\cos^{2}(\frac{\mu}{2})+\sin^{2}(\frac{\mu}{2})]-4\cdot \sin^{2}(\frac{\epsilon}{2})}{2\cdot \cos(\frac{\mu}{2})} &\text{Rearrange figures}\\
&=\frac{1+[1]-4\cdot \sin^{2}(\frac{\epsilon}{2})}{2\cdot \cos(\frac{\mu}{2})} &\text{cos²α + sin²α = 1}\\
&=\frac{2-4\cdot \sin^{2}(\frac{\epsilon}{2})}{2\cdot \cos(\frac{\mu}{2})}\\
&=\frac{1-2\cdot \sin^{2}(\frac{\epsilon}{2})}{\cos(\frac{\mu}{2})}\\
&=\frac{\cos(\epsilon)}{\cos(\frac{\mu}{2})} & \text{1-2sin²α = cos 2α}
\end{align}}$$
We can now use this new formula to double check our work on the truncated icosahedron. Hexagons have exterior angles of 120° (ε) and pentagons are 108° (μ). So we get:
$$cos\theta=\frac{\cos(120)}{\cos(\frac{108}{2})}=\frac{cos(120)}{cos(54)}\\ \theta=148.2825256\ldots^\circ$$
The formula can be used to quickly find the vertex edge angle of any of the Platonic or Archimedean solids that have only 3 shapes meeting at each vertex, with 2 (or all 3) of them the same. (Although it isn’t as much fun as actually working it out ourselves.) It can also be used on prisms, but that is trivial, as the edge will always be at 90° to the bases.
We can find the angle made by slicing the pyramid through ΔCDE, but the result really doesn’t mean much as the plane made by ΔCDE is not perpendicular to the plane made by the base. ΔADG is perpendicular to the base plane. There would be 2 angles needed to describe the result. Example, looking at the truncated icosahedron, you can see the edges splaying out from the pentagons even with the center lines, sort of like the spokes of a wheel, but looking at the hexagons, the edges don’t line up with the center lines, they are slightly off.
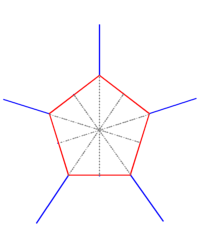
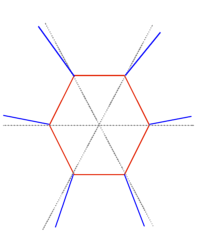
Likewise, in a pyramid with all 3 apex angles different, there would be no cross section that was perpendicular to the base plane, so no real usage here.