
I started off posting about the truncated icosahedron, despite being fairly complex compared to the platonic solids, like the tetrahedron.
The regular tetrahedron is probably the simplest 3D shape, except for maybe the sphere. It is made of 4 equilateral triangles, forming a triangular pyramid.
Starting with a tetrahedron with vertexes named A, B, C, & D, with D as the apex (fig. 1), we can bisect ΔABC from point A to line BC and call that point G (fig. 2).
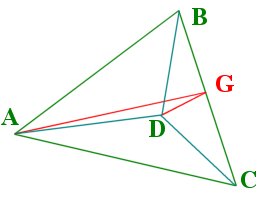 Figure 1 |
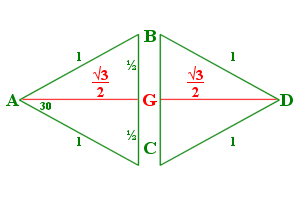 Figure 2 |
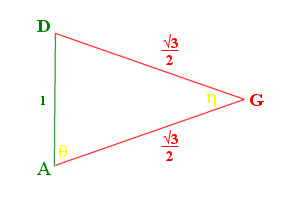 Figure 3 |
The bisection of ΔDBC would follow the same, a line DG would also equal AG. Figure 3 shows the cross section of the tetrahedron, ΔADG. We can then use the law of cosines to find ∠θ and ∠η.
\(\Large\cos \eta = \frac{AG^{2} + DG^{2} – AD^{2}}{2\cdot AG \cdot DG} = \frac{\frac34 + \frac34 – 1}{2\cdot\frac{\sqrt{3}}{2}\cdot\frac{\sqrt{3}}{2}} = \frac{\frac24}{\frac64} = \frac13\).
The angle (η) between each face, the dihedral angle, is \(cos^{-1} (\frac{1}{3})=70.528779\ldots^\circ\).
\(\Large\cos \theta = \frac{AG^{2} + AD^{2} – DG^{2}}{2\cdot AG \cdot AD} = \frac{\frac34 + 1 – \frac34}{2\cdot 1\cdot\frac{\sqrt{3}}{2}} = \frac{1}{\sqrt3}\).
The angle that the edge to face (θ) makes would be \(cos^{-1}\frac{1}{\sqrt{3}}= 54.73561\ldots^\circ\). Also since ΔADG is isosceles, ∠ADG = ∠DAG = θ.
\(2\cdot\theta+\eta=180^\circ\)
From the above equations and figures, you can then calculate other aspects, such as the height.
But what about non-regular tetrahedra? Let’s think about other pyramids, both fat and short and tall and thin. All the triangles in the regular tetrahedron have three 60° corners.
Let’s suppose that the angles originating at point D are all equal (we will call them λ), and the edges are also equal (we will call them length 1). We would have something like that of a camera tripod.
If we spread the legs, the camera will get lower to the ground and if we bring the legs together, the camera will get higher. The same is true of our pyramid.
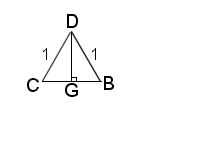 Figure 4 |
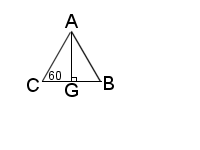 Figure 5 |
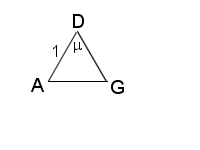 Figure 6 |
Let us again bisect the angles λ, as shown in fig. 4.
\( BG = CG= \sin(\frac{\lambda}{2})\), \( BC= 2\cdot \sin(\frac{\lambda}{2})\), \( DG= \cos(\frac{\lambda}{2})\).
Looking at the pyramid’s base ΔABC (fig. 5), \(BC = AC= AB = 2\cdot \sin(\frac{\lambda}{2})\), then \(AG = BG\cdot\sqrt{3} = \sqrt{3}\cdot sin(\frac{\lambda}{2})\).
We again us the law of cosines to find μ (fig. 6).
\(\Large\cos\mu=\frac{1+cos^{2}\frac{\lambda}{2} – 3\cdot sin^{2}\frac{\lambda}{2}}{2\cdot cos\frac{\lambda}{2}}\)
If we add \((1\cdot sin^{2}\frac{\lambda}{2} -1\cdot sin^{2}\frac{\lambda}{2})\), which equals zero, to the top of the equation, we get \(\large\cos\mu=\frac{1+(cos^{2}\frac{\lambda}{2}) – 4\cdot sin^{2}\frac{\lambda}{2}+(sin^{2}\frac{\lambda}{2})}{2\cdot cos\frac{\lambda}{2}}\). Note the change of the three to four.
The items in parentheses can be combined using the identity cos² α + sin² α = 1:
\(\Large\cos\mu=\frac{1+1-4\cdot sin^{2}\frac{\lambda}{2}}{2\cdot cos\frac{\lambda}{2}}=\frac{2-4\cdot sin^{2}\frac{\lambda}{2}}{2\cdot cos\frac{\lambda}{2}}=\frac{1-2\cdot sin^{2}\frac{\lambda}{2}}{cos\frac{\lambda}{2}}\).
Using the identity cos 2α = 1 – 2·sin² α, gives: \(\large\cos\mu=\frac{cos\lambda}{cos\frac{\lambda}{2}}\).
We can then use this formula to verify the regular tetrahedron’s vertex edge angle that we found earlier. If \(\lambda=60^\circ\), \(\large\cos\mu=\frac{cos60}{cos30}=\frac{\frac12}{\frac{\sqrt{3}}{2}}=\frac{1}{\sqrt{3}}\), which is the same as θ above.
This formula can also be used on other polyhedra where there are three identical angles joining at a vertex, such as the cube,\(\large\cos\mu=\frac{cos90}{cos45}=\frac{0}{\frac{1}{\sqrt2}}=0, \mu=90^\circ\) or dodecahedron, \(\large\cos\mu=\frac{cos108}{cos54}=\frac{\frac{1-\sqrt5}{4}}{\frac{\sqrt{10-2\sqrt5}}{4}}=\frac{1-\sqrt5}{\sqrt{10-2\sqrt5}}, \mu=121.71747^\circ\).
I will get to the dodecahedron soon. The cube is so easy to figure out mathematically, rather boring.
Next posting, I will show you what happens if the pyramid leans a bit, that is if one of the apex angles is different that the other two.